Titan97
Gold Member
- 450
- 18
Divergence can be defined as the net outward flux per unit volume and can be explained using Gauss' theorem. (I read this in Feynman lectures Vol. 2)
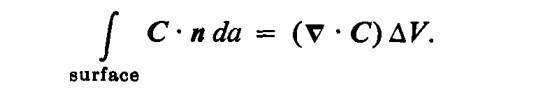
In the next page, He derives Stokes' theorem using small squares.
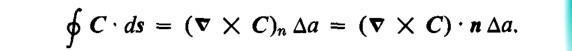
The left side of equation represents the total circulation of a vector field along a closed path S.
The right side contains the component of Curl perpendicular to ##\Delta a##
This only gives meaning to a particular component of Curl. How can I explain Curl using stokes' theorem just like how divergence is explained?
In the next page, He derives Stokes' theorem using small squares.
The left side of equation represents the total circulation of a vector field along a closed path S.
The right side contains the component of Curl perpendicular to ##\Delta a##
This only gives meaning to a particular component of Curl. How can I explain Curl using stokes' theorem just like how divergence is explained?