Measurable Functions .... Lindstrom, Proposition 7.3.7 .... ....

[Math Amateur]

TL;DR

I need help with Tom Lindstrom's proof that if f and g are measurable then so is f + g ...

I am reading Tom L. Lindstrom's book: Spaces: An Introduction to Real Analysis ... and I am focused on Chapter 7: Measure and Integration ...

I need help with the proof of Proposition 7.3.7 ...

Proposition 7.3.7 and its proof read as follows:

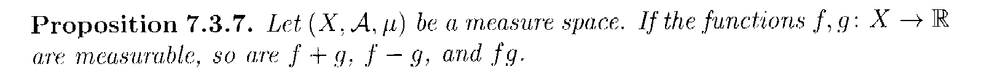
In the above proof by Lindstrom we read the following:

" ... ... $(f + g)^{ -1} ( [ - \infty , r ) ) = \{ x \in X | (f + g) \lt r \}$

$= \bigcup_{ q \in \mathbb{Q} } ( \{ x \in X | f(x) \lt q \} \cap \{ x \in X | g \lt r - q \} )$ ... ... "Can someone please demonstrate, formally and rigorously, how/why ...

$\{ x \in X | (f + g) \lt r \} = \bigcup_{ q \in \mathbb{Q} } ( \{ x \in X | f(x) \lt q \} \cap \{ x \in X | g \lt r - q \} )$ ... ...
Help will be much appreciated ...

Peter=============================================================================================================Readers of the above post may be assisted by access to Lindstrom's introduction to measurable functions (especially Lindstrom's definition of a measurable function, Definition 7.3.1) ... so I am providing access to the relevant text ... as follows:

Hope that helps ...

Peter

 

[member 587159]

$\subseteq$

Given $f(x)+g(x)< r$, use density of the rational numbers in the real numbers to choose $q\in \mathbb{Q}$ with $f(x)< q < r- g(x)$.

$\supseteq$

Is trivial.

 

[Math Amateur]

Sorry ... but i don't follow ... not completely anyway ...

Apologies for being a bit slow ...

Peter

 

[member 587159]

Sorry ... but i don't follow ... not completely anyway ...

Apologies for being a bit slow ...

Peter

Refresh the page ( I made an edit). What don't you understand?

 

[Math Amateur]

Hmmm ... we require $\{ x \in X | (f + g) (x) \lt r \}$ to be measurable for all $r \in \mathbb{R}$ ... ... surely this is true because $(f + g)(x) = f(x) + g(x)$ and $f$ and $g$ are measurable ...

So why do we have to invoke the density of the rationals ...

Can you try to make more clear what is going on ...?

Peter

EDIT ... cannot understand what has gone wrong with my Latex code

 

[member 587159]

Hmmm ... we require $\{ x \in X | (f + g) (x) \lt r \}$ to be measurable for all $r \in \mathbb{R}$ ... ... surely this is true because $(f + g)(x) = f(x) + g(x)$ and $f$ and $g$ are measurable ...

So why do we have to invoke the density of the rationals ...

Can you try to make more clear what is going on ...?

Peter

That's another question than the one you asked!

However, you are exactly trying to prove that $f+g$ is measurable when $f$ and $g$ are. To check measurability, you have to show that (note my superior notation) $\{f+g < r\}$ is a measurable set for all $r$. The proof then writes $\{f +g < r\}$ as a countable union of measurable sets, to deduce that $\{f+g< r\}$ is measurable. For this, the hypothesis that $f$ and $g$ are measurable is used. This countable aspect is very important: the uncountable union of measurable sets need not be measurable.

 

[member 587159]

Note however, there is an alternative proof. You can prove that addition $+: \mathbb{R}^2 \to \mathbb{R}$ is measurable (because it is continuous) and you can also quickly prove that composition of measurable functions is measurable. Hence, if $f,g$ are measurable, then so is $f+g = + \circ (f,g)$.

Also, there seems to be some bugs with the Latex code for me as well. Try to refresh the pages when you are done editing.

 

[Math Amateur]

Thanks ... can definitely see the point about countability ... and also that f < q < r - g implies that ... f < q and (intersect) g < r - q is the case ...

Peter

 

[member 587159]

Thanks ... can definitely see the point about countability ... and also that f < q < r - g implies that ... f < q and (intersect) g < r - q is the case ...

Peter

Then is your problem solved or are there any other issues left?

 

[Math Amateur]

Still reflecting on things ... but think issues are resolved ...

Most grateful for your help ...

Thanks again ...

Peter

 

[Math Amateur]

I have been reflecting further on proving that $f+ g$ is measurable when $f$ and $g$ are measurable ... and I need to clarify an issue ... ...

I need to understand exactly what is wrong with the following argument ... something surely is wrong because the proof doesn't involve ranging over $\mathbb{Q}$ ...

... ... ... the argument follows ... ...First note that $f + g \lt r$

$\Longrightarrow$ there exists $q \in \mathbb{Q}$ such that $f \lt q \lt r - g$

$\Longrightarrow f \lt q$ and $g \lt r - q$

$\Longrightarrow$ for all $x \in X$ we have $f(x) \lt q$ and $g(x) \lt r - q$

Thus $\{ x \in X \ | \ (f + g) \lt r \} = \{ x \in X \ | \ f(x) \lt q \} \cap \{ x \in X \ | \ g(x) \lt r - q \}$Can someone please clarify what is wrong with the above argument ...
Help will be much appreciated ...

Peter

 

[Infrared]

First note that $f + g \lt r$

$\Longrightarrow$ there exists $q \in \mathbb{Q}$ such that $f \lt q \lt r - g$

This isn't right (and I'll admit the given proof glosses over this point a little bit), because $f$ and $g$ are functions. For example, suppose $f(x)=x$ and $g(x)=-x$ and let $r=1.$ Then $0=f(x)+g(x)<1=r$ is true for all $x$, but there is no $q$ such that $f(x)<q$ for all $x$.

A little more conceptually: the given proof is saying that for every $x$, there is some $q\in\mathbb{Q}$ (depending on $x$) such that $f(x)<q$ and $g(x)<r-q$. That $q$ may need to depend on $x$ is why a union over all rationals is needed. You are trying to escape the dependence on $x$.

 

[Math Amateur]

This isn't right (and I'll admit the given proof glosses over this point a little bit), because $f$ and $g$ are functions. For example, suppose $f(x)=x$ and $g(x)=-x$ and let $r=1.$ Then $0=f(x)+g(x)<1=r$ is true for all $x$, but there is no $q$ such that $f(x)<q$ for all $x$.

A little more conceptually: the given proof is saying that for every $x$, there is some $q\in\mathbb{Q}$ (depending on $x$) such that $f(x)<q$ and $g(x)<r-q$. That $q$ may need to depend on $x$ is why a union over all rationals is needed. You are trying to escape the dependence on $x$.

Thanks for the help Infrared ...

I can see $q$ may depend on $x$ ... but cannot see why a union over all \mathbb{Q} resolves this issue ...

... why are we justified in taking a union over all $\mathbb{Q}$ ...

Can you explain further ...

Peter

 

[member 587159]

Let's formally show that $$\{f+g < r\}= \bigcup_{q \in\mathbb{Q}}\{f < q\} \cap \{g < r-q\}$$
Suppose that $x \in \{f+g < r\}$. Thus $f(x) + g(x) < r$, so $f(x) < r-g(x)$. By density of $\mathbb{Q}$ in $\mathbb{R}$, we can pick $q(x) \in \mathbb{Q}$ (note the $x$-dependency) such that $f(x)< q(x) < r-g(x)$. Then clearly we have $x \in \{f< q(x)\}\cap \{g < r-q(x)\} \subseteq \bigcup_{q \in \mathbb{Q}} \{f < q\}\cap \{g< r-q\}$. This shows
$$\{f+g < r\}\subseteq \bigcup_{q \in \mathbb{Q}} \{f< q\}\cap \{g < r-q\}$$
Next, suppose $x \in \bigcup_{q \in \mathbb{Q}} \{f< q\}\cap \{g < r-q\}$. Then there is $q(x) \in \mathbb{Q}$ with $f(x)< q(x)$ and $g(x) < r-q(x)$. Then $f(x) + g(x) < q(x) + r-q(x) = r$ and thus $x \in \{f+g < r\}$. This shows
$$\bigcup_{q \in \mathbb{Q}} \{f< q\}\cap \{g < r-q\}\subseteq \{f+g < r\}$$

 

[Math Amateur]

Hi Math_QED ...

Thank you for an exceedingly clear and helpful post ...

That resolves all issues ...

Thanks again ...

Peter