Mechanical Advantage of a 4-bar

[gocomando]

Alright, the problem at a glance is rather simple: find the mechanical advantage at two given values of θ2.

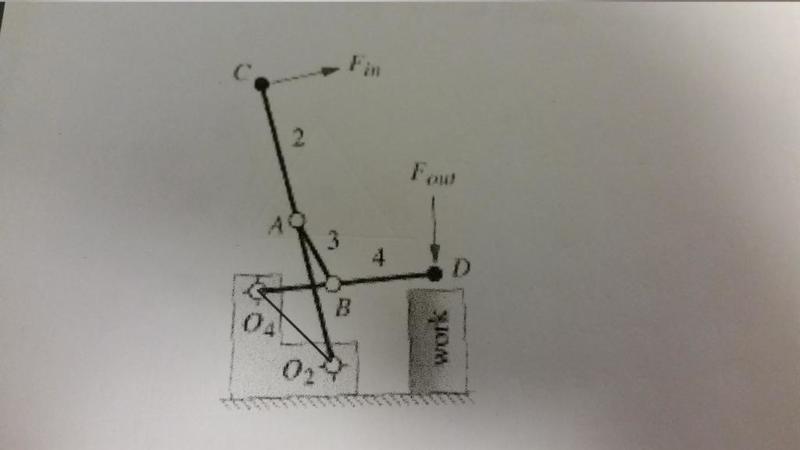
Given:
rO2A = r2
r02C = rin
rAB = r3
rO4B = r4
rO4D = rout
rO2O4 = r1
θ1 = 135°

Find:
Mechanical advantage when θ2 is equal to 104°, and when θ2 is equal to 91°.

Equations to use:
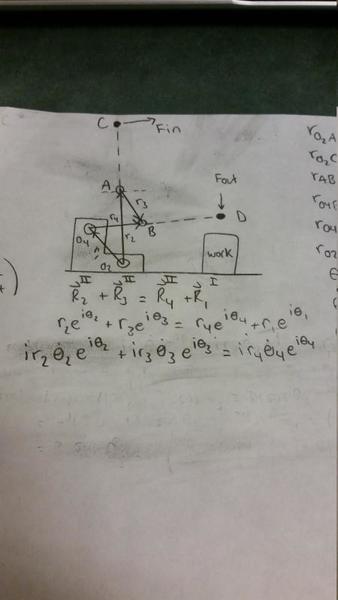
Mech advantage = (rin/rout) * (ωin/ωout) (I think this is the one I'm supposed to use)EDIT: Turns out we're allowed to simply measure the actual angle provided in the problem. Now, since this 4-bar is inverted, how exactly do I measure the angle θ3 andθ4?

EDIT: I believe I'm supposed to measure from the positive x-axis counterclockwise until I get to the link. Using this, I got θ3= -57 and θ4 = 187. From here though, how might I find (ωin/ωout)? I have the vector loop equation R2 + R3 = R4 + R1, and when I get the corresponding velocity equations, R4 is in there making things complicated.

 

[Greg Bernhardt]

Thanks for the post! Sorry you aren't generating responses at the moment. Do you have any further information, come to any new conclusions or is it possible to reword the post?

 

[Dr.D]

The original figure is poorly drawn. If Fin is as shown, then the equilibrating force on the linkage at D must be upward, opposite the direction shown.

Do you know the method of virtual work for statics? This problem is a natural for that method.