Analyzing the Mechanics of a Wobble Plate in a Cranked Axle Mechanism

[noname12345]

TL;DR Summary

I have a moderately complex mechanism, that I need to construct a kinematics diagram for, and then derive a parametrised equation for the resultant forces, but a solution is escaping me.

In the following cross section, the static guide plate (light blue) is rigidly constrained, fixed to the body (not shown) of the mechanism. It serves as the mounting point for a cranked axle (dark blue) via a combination thrust and radial bearing (pink & yellow) that constrains it to a single freedom, rotation around the vertical Z-axis.

The upper end of the axle is cranked (as shown, to 15deg), and a "wobble plate" (purple) is mounted to that via another combination of thrust and radial bearing such that the cranked axle and wobble plate can freely rotate with respect to each other around the cranked axle axis.

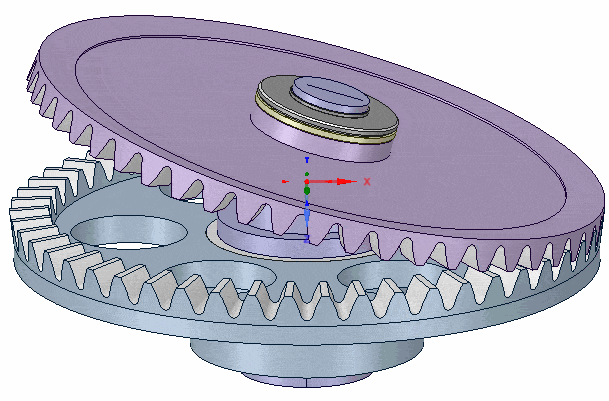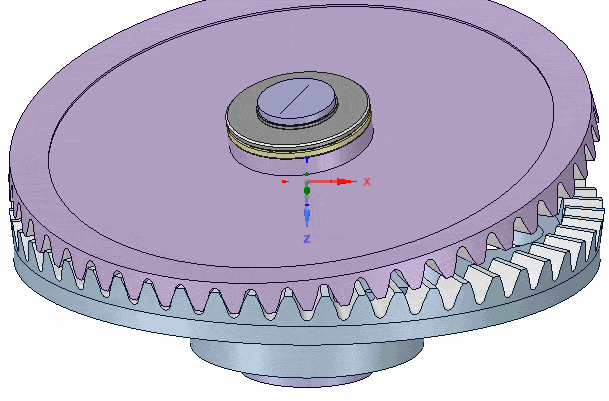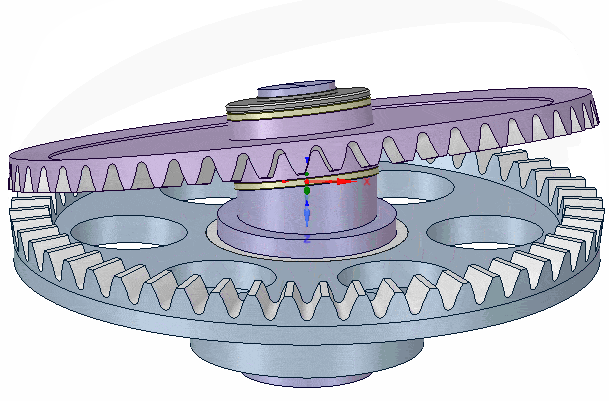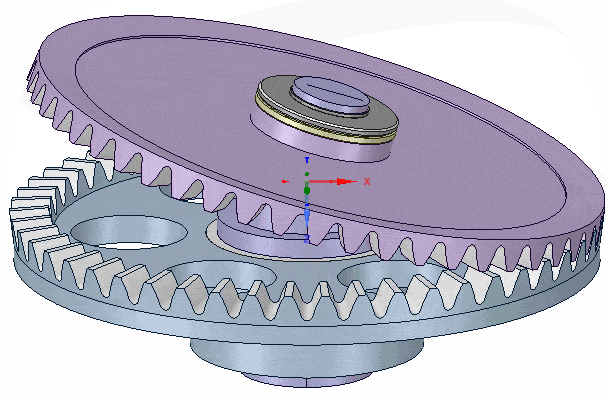
However, the outer edge of the wobble plate carries a 50 tooth bevelled gear that engages with another bevel gear (also 50 tooth) on the static guide plate, thus the wobble plate cannot rotate with respect to that guide plate.

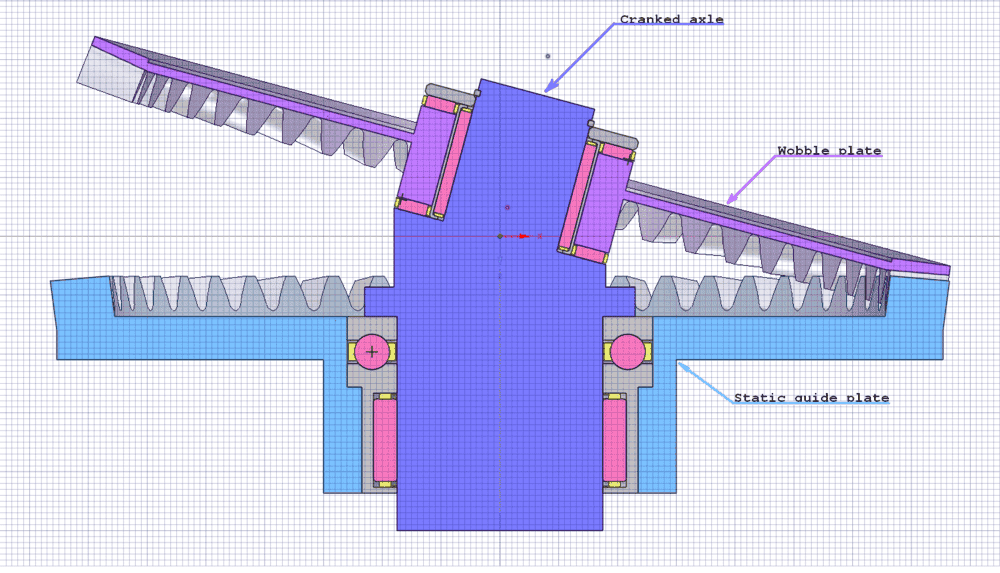
If a torque is applied to the bottom end of the axle, the cranked part imparts forces (via the upper bearings) to the wobble plate, and the combined action of those forces and its engagement with the guide plate gear, causes the wobble plate to wobble (or rock or nutate) in-place. That is, the equal number of teeth on the gears mean it does not rotate with respect to the static guide plate, but rather 'rolls' around the periphery, a little like a spinning coin at the end of the spin, just before it looses momentum and falls flat on the table.

Having described the mechanism -- hopefully clearly -- now the problem I am trying to solve.

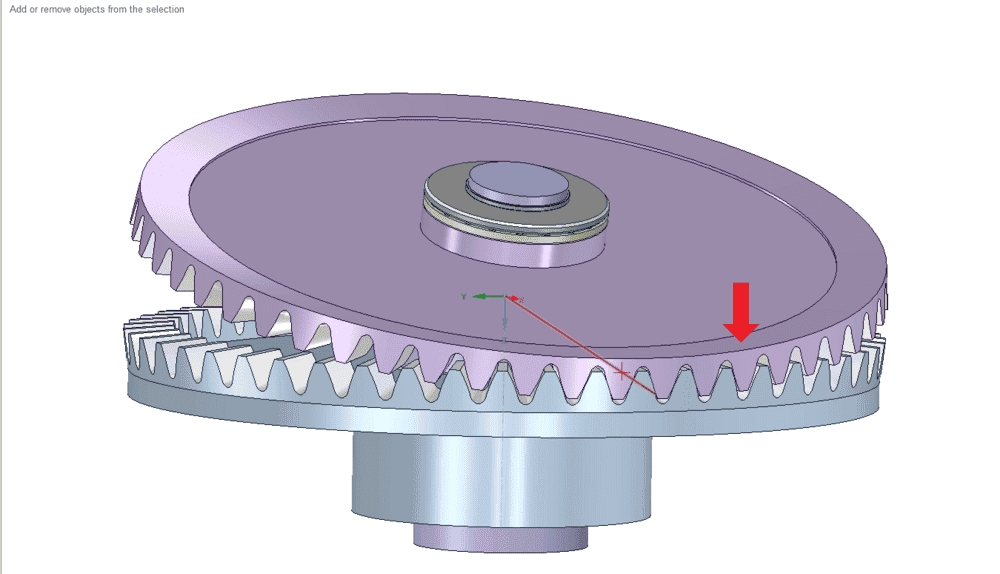
If a force is applied to the periphery of the wobble plate at the thick red arrow, the plate will attempt to rotate around the pitch point axis (thin red line) of the currently engaged tooth. In order for that to happen, the cranked axle will have to rotate relative to the wobble plate, (and the un-cranked part of the axle will rotate relative to the static guide plate).

My goal is to work out how much torque is generate at the output end (bottom) of the axle, for a given force applied to the wobble plate periphery.

And further, to derive a parametrised equation that allows me to calculate that torque for different combinations of a) input force; b) plate diameter; c) crank angle.

My best attempt at a kinematics diagram looks like this:

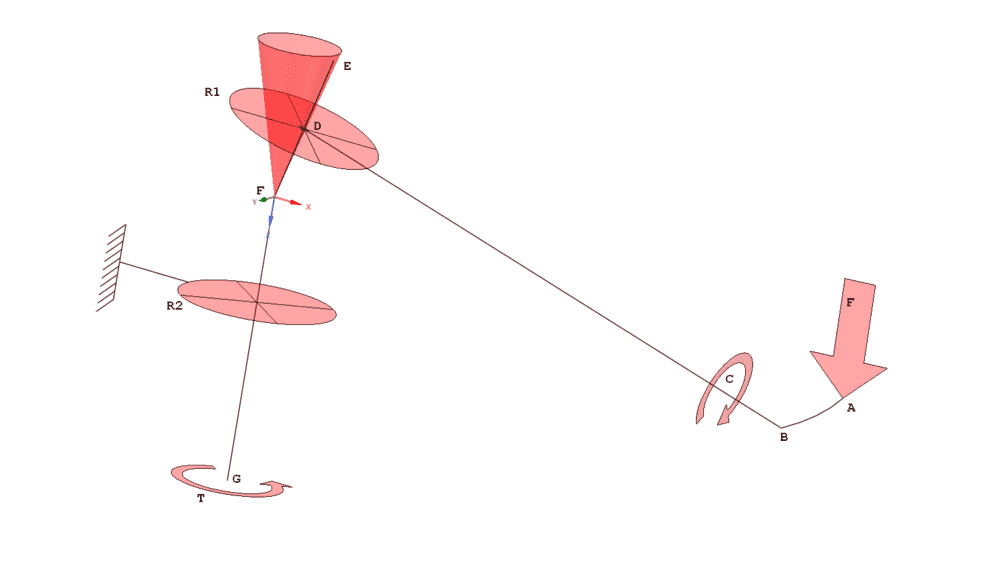
Description:

A force F, acting at some distance AB around the periphery of the wobble plate from the pitch point of the currently engaged tooth B, acts as a lever, and creates a torque C, around the radial pitch axis BD.

That torque (somehow?) imparts a force (what?) on the cranked axle EF (running in bearing R1), which in turn induces a torque T, in the nominal axle FG (running in bearing R2).

Any and all cluebats, hints, references gratefully received.

If anything is unclear please ask questions.

Thanks, Buk.

Note: This is not homework, but rather a retired, one-time engineer trying to recall/re-learn stuff that I barely made use of in the 40+ years since I learned it, to solve or disprove a pet notion I been kicking around in my head for about 30 years.

(It's amazing the things we do to while away the long hours of the lock-down.)

 

[jrmichler]

Any and all cluebats, hints, references gratefully received.

Search nutating disk.

 

[noname12345]

Search nutating disk.

Thanks for the very interesting sidetrack. Whilst that is certainly a very similar mechanism, my search didn't lead me to anything that helped me to solve my primary question about the kinematics.

 

[jrmichler]

I searched kinematic diagram, and found this: https://me-mechanicalengineering.com/kinematic-diagrams/. But your question appears to be how to calculate the torque on shaft FG from a force F rather than how to construct a kinematic diagram. Your existing diagram, while not exactly like the kinematic diagrams shown in the link, should be good enough to calculate the shaft torque.

You are applying a torque C to link BD, and that torque has a component parallel to shaft FG. Torque is a vector that can be resolved into components exactly like force vectors.

Hint: Look at extreme cases, specifically shaft bend angles of zero (straight shaft) and 90 degrees.

Hint: If you have thoughts of building it, look into opposed angular contact or tapered roller bearings. Your shaft bearings will have high moment loads that needle bearings cannot support.

engineer trying to recall/re-learn stuff that I barely made use of in the 40+ years since I learned it

THUMBUP

 

[noname12345]

You are applying a torque C to link BD, and that torque has a component parallel to shaft FG. Torque is a vector that can be resolved into components exactly like force vectors.

The problem is, as best as I can figure, the components of torque C cancel each other out.

That is, the torque C, tries to revolve the top and bottom edges of the bearing against the cranked axle in shear, in equal and opposite amounts. And I fail to see how that torque is applied to the axle?

However, the force F, also acts to roll the wobble disk gear teeth around the static guide plate gear teeth, providing a thrust around the cranked axial plane:

And of course, as soon as the axle revolves even the slightest amount, the mesh point between the gears rotates, and the centre of rotation of the torque C rotates, so the length of the moment arm AB shortens, and everything changes.

So I'm finding it very difficult to work out how much of the input force is wasted in trying to shear the axle shaft, and how much gets translated into torque of the output shaft?

Hint: If you have thoughts of building it, look into opposed angular contact or tapered roller bearings. Your shaft bearings will have high moment loads that needle bearings cannot support.

The disks are only 100mm diameter, and the shafts ~20mm, so space precludes the use of opposed taper rollers (or angular contact or deep groove) bearings; hence the full complement needle roller bearing to handle the radial loads and a pair of pre-loaded needle roller thrust bearings for the thrust components.

The alternative would be to use plain journal bearings, but this isn't intended to be a high torque mechanism -- 40Nm is a upper goal -- but at 4000rpm, plain bearings would be less efficient than desired.

 

[jrmichler]

Looking at the bent shaft in your kinematic diagram in Post #1, and the torque C applied to it by the force F on moment arm AB:

A torque (moment) applied to one location has the same magnitude if treated as applied to a different location. Since a moment is a vector quantity, it can be decomposed into components. In this case, you are interested in the component parallel to the lower portion of the bent shaft because that is the torque on that shaft. The torque component perpendicular to the lower portion of the bent shaft is the moment that the bearing must support. The math is basic trigonometry.

The moment C is the force F times the perpendicular distance from line BD to point A, not the arc length AB.

Plain bearings can be very efficient at 4000 RPM. Search Stribeck curve, and design the bearing such that, with the correct lubricant viscosity, it will operate in the full fluid film portion of the curve. Just be very careful about the moment load on the bearing. A pair of well separated bearings may be needed.

 

[Dr.D]

I think the OP is correct to focus on the kinematics, rather than to leap to a force analysis. If the kinematics are well understood, then virtual work will give give the force relation easily.

 

[noname12345]

Looking at the bent shaft in your kinematic diagram in Post #1, and the torque C applied to it by the force F on moment arm AB:
View attachment 261341
A torque (moment) applied to one location has the same magnitude if treated as applied to a different location. Since a moment is a vector quantity, it can be decomposed into components. In this case, you are interested in the component parallel to the lower portion of the bent shaft because that is the torque on that shaft. The torque component perpendicular to the lower portion of the bent shaft is the moment that the bearing must support. The math is basic trigonometry.

The moment C is the force F times the perpendicular distance from line BD to point A, not the arc length AB.

Maybe I am misunderstanding you and your diagram, but there is no way to decompose a torque around an axis, into two vectors orthogonal to that axis.

My interpretation of the way you have shown the torque acting on the cranked axle is that the entire axle would be trying to rotate around the axis of the torque:

As in https://www.physicsforums.com/attachments/1587730106178-png.261319/

You also appear to be forgetting the bearing(s).

Plain bearings can be very efficient at 4000 RPM. Search Stribeck curve, and design the bearing such that, with the correct lubricant viscosity, it will operate in the full fluid film portion of the curve. Just be very careful about the moment load on the bearing. A pair of well separated bearings may be needed.

It is well-documented that under like-for-like -- load, speed and tribological conditions -- a plain bearing has 3 times higher friction than a rolling element bearing.

Whilst modern composite plain bearings can have exceptionally low friction when running at their optimum design speed and loading; that optimum constitutes a very small window of the range of operating conditions and the efficiency is far less outside of it. For example, startup friction for a plain bearing is 30 to 60 times higher than for a rolling element bearing.

As the application is characterised by constantly varying speed (from 0rpm through ~4000rpm), and constantly varying loading from negative maximum through positive maximum and back again; the efficiency requirements do not lend themselves to plain bearing use.

 

[jack action]

This is how I see it (ignore anything that is not a pink arrow):

Your force F is counterbalance by the vertical arrow that acts either at the gear contact or by the bent shaft (or a mix of both). The torque created will be counterbalance by the one created by the horizontal arrows, one acting at the teeth contact point and the other acting on the bent shaft, in the background (assume a perfect bearing that only rotate without bending).

Now, looking only at the bent shaft (in a perpendicular plane, top view), this horizontal force is acting on it with an offset from the center of rotation, thus inducing a driving torque on the bent shaft.

 

[noname12345]

Now, looking only at the bent shaft (in a perpendicular plane, top view), this horizontal force is acting on it with an offset from the center of rotation, thus inducing a driving torque on the bent shaft.

Thank you! I've reached a somewhat different conclusion to you, but the train of thought was absolutely triggered by your response.

I still think that the torque acting on the cranked part of the axle produces a net zero reaction. In the frame of reference of the cranked axle, the torque acting around the line of contact of the gear teeth imparts equal and opposite forces on the axle:

However, the cranked portion of the axle has no possibility of moving without the uncranked (hereafter "main") axle moving also anyway, so we have to consider those forces (the resultants of the torque split 50-50) acting in the frame of reference of the main axle, and as you point out, in that frame, the distances from the fulcrum (main axle axis) at which the split force acts, are no longer equal.

But, torque is force *distance, and if the torque is split 50-50, the force acting at the shorter distance, will be greater than the force acting at the greater distance, but each pair of force*distance will be 50% of the total torque again resulting in a net zero reaction. (I think!)

The thing I have been ignoring/forgetting, is that the contact between gear teeth is not a point contact, but rather a (theoretically, if we could assume perfect gear pair manufacture and assembly with zero tolerances and perfect surface finish) line contact. And in the reality, with toleranced imperfections, profile modifications and elastic deformation, we have contact patch:

And that contact patch is (at least theoretically) self-bearing.

So if we have a force acting on the upper gear at the red arrow, and the red dotted line is the theoretical contact line between the two gears, the we effectively have the forces being transmitted between the two gears through a triangular lever/link/plane like so:

And we don't need to consider any force transfer to the axle directly. As the bottom gear is fixed in place, as the line of contact rolls down the involute profile, the only result is that upper gear must move.

Of course, for that to happen, the axle will have to revolve, and the two bearings will revolve by differing amounts to accommodate the combined revolve of the axle and tilt of the upper gear, but (again, I think) the major part of the force acting (notionally) at the centre of the tooth faces and in the direction of the long horizontal red arrow; and a minor part acting downward (short red arrow) being absorbed (and wasted) by the fixed bottom gear.

Which makes the value of the torque transferred to the main axle, the horizontal component * the distance from the centre of the tooth face to the axis of the main axle.

I still need to figure out the effect of the gear's pressure angle on the split of the force into its horizontal and vertical components; but that should allow me to arrive at a relatively simple formula to relate the input force value and position, and the tilt angle of the upper gear, to the output torque (ignoring bearing friction losses et al.).

Thank you for your reply. Feel free to pull my analysis apart :)

Buk.

 

[noname12345]

I just noticed that the "red dotted line" I referred to in the text above was omitted from the image I posted. Here's that corrected.