- #1
AlonZ
- 8
- 0
- Homework Statement
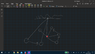
- Need to find the angle from which a pendulum with the length L that reaches its lowest point will complete a full circle around a pivot which distance is from the lowest point is l
- Relevant Equations
- assume Tension at the highest point of the loop is 0, because that's the minimun for a full loop.
My, supposedly rational thought is that if the pendulum will drop from a height higher than the top of the loop's height, by the law of conservation of energy, it'll have enough velocity to complete the loop.
The teacher's final result shows a different approach.
Am I right? Wrong? Thanks
The teacher's final result shows a different approach.
Am I right? Wrong? Thanks