Method of Images Question (Concave Geometries)

[^_^physicist]

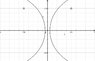
I've been working with image charges for a while now, and I have noticed that I haven't been able to find a single discussion on the use of image charges for concave geometries (i.e. a charge on the "inside" of a catenary shaped curved conducting plate, see attached picture). Has anyone worked with a problems of this nature before? Anyone know of any resources that discuss problems of this nature? I have been racking my brain for a over a few days and I can't seem to figure out how to a approach a problem like this. I almost just broken down and tried to solve these geometries with boundary conditions and the laplace/possion equations (depending on the problem), but they become a mess way to quickly.

Any help is appreciated.

(A note on the picture, the point on the right is a negative charge and the point on the right is a positive charge. I am very concerned with this problem for a research project; however, I would be just as happy (in fact more so) if someone could give an explanation for solving the simplified problem of just looking at the left-hand side (or right-hand side) of the graph)

 

[marcusl]

Most geometries cannot be solved with images. Cylinders, planes, wedges and spheres are the cases that are known. If your curve possesses a transformation to a line or circle (I doubt catenaries qualify), you might have a chance using conformal mapping techniques. Weber's book Electromagnetic Fields covers this, also Smythe.

 

[^_^physicist]

Well a semi-reasonable approximation to the catenary shape is that of a hyperbola (at least at distances close enough to the hyperbola, and since my problem is with something close enough to the catenary anyway, I am not too concerned with making this substitution).

I don't have much experience (i.e. no experience) with conformal mapping, so would a hyperbola be a something we could work with? Heck would any conic section be something that would work well with conformal mapping. (Also, thanks for the recommendation on the Weber book, I am picking it up today).