Michelson Morley experiment: relativistic explanation

[crick]

I don't uderstand how, using special relativity theory (time dilatation and length contraction), one can explain why in the Michelson interferometer there is no delay between the two rays in the reference frame where the interferometer is moving. Consider the picture $2.$

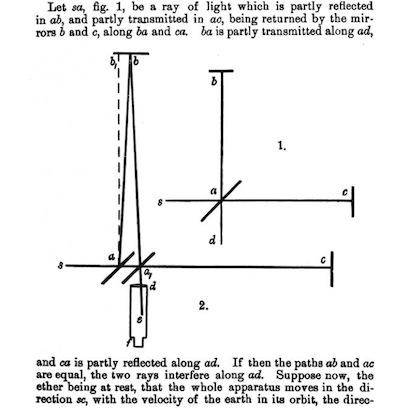Setting $ab_1=ac=L$ and $\gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$ ($v$ is the velocity of the interferometer), the time taken for path $aba_1$ should be
$$t_1=\frac{2L}{c}\gamma$$For the other ray the path length should be $aca$ (but it's contracted), therefore

$$t_2=\frac{2L}{c}\frac{1}{\gamma}$$How can possibly be $t_1=t_2$?

 

[Orodruin]

In the second case you are missing the fact that the time taken is not the length divided by c. The apparatus is moving!

 

[Dale]

For the other ray the path length should be aca (but it's contracted)

Dont forget that the mirrors are moving, so the path length is different from the apparatus length.

 

[Janus]

This animation might help: