Spathi
Gold Member
- 102
- 10
- TL;DR
- PBCs mean that the atoms with e.g. fractional coordinates (0.0;0.0;0.0) and (1.0;0.0;0.0) are equivalent. PBCs in crystals are specified by three lattice vectors A, B, C...
I work in the field of quantum chemistry, in particular computations with periodic boundary conditions (PBC) needed for crystallographers. The crystallography data is usually presented as a set of fractional coordinates which are recounted to Cartesian ones. In the fractional coordinates, each cell of a crystal is a cube, e.g. the atoms in molecule belonging to the first cell have the coordinates from 0.0 to 1.0. Some real crystals have cubic cells too, e.g. NaCl:
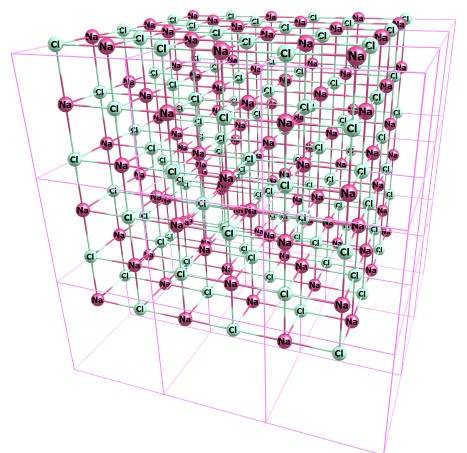
PBCs mean that the atoms with e.g. fractional coordinates (0.0;0.0;0.0) and (1.0;0.0;0.0) are equivalent. PBCs in crystals are specified by three lattice vectors A, B, C; e.g. for NaCl above these vectors are three orthogonal vectors with length 5.4533 Angs each (this also mean that the crystallography parameters are: a=5.4533, b=5.4533, c=5.4533, alpha=90, beta=90, gamma=90). At the same time, for each crystal, in fact there must be an unlimited numbers of possible lattice vectors. This can be illustrated by a 2-d example:

Here the trivial PBC parameters are (1.0; 0.0) and (0.0;1.0), but also we can build the lattice vectors (3.0; -1.0) and (1.0; 3.0), which describe the same crystal.
I try to implement building the Miller indices in my program Chemcraft. Firstly the user specifies three integer numbers, e.g. 1 1 1, which mean that the new vector C will be (1.0; 1.0; 1.0) in fractional coordinates. My question is, how to build the A and B vectors if we know C. This is similar to the 2d task above, but evidently more difficult.
As far as I understand, the A and B vectors can be built in different ways; they must be orthogonal to C, maybe to each other too, but they still can be rotated along the C vector. And they must be still integers, if I understand correctly, and they must define the same crystal as it was. This can be illustrated by the 2d picture above – if the first lattice vector A=(3.0; -1.0), the second can be only B=(1.0; 3.0) to keep the same crystal.
So how can these integers A and B (3 digits for each) be obtained, if we know C?
The new values of A, B, C in terms of old (9 numbers) can be entered in the window “Redefine lattice” in Materials Studio program, I have implemented the same in Chemcraft. I suppose, to build the Miller index 1 1 1, we should specify these lattice redefinition parameters:
A: 0 1 -1
B: -1 1 0
C: 1 1 1
With these parameters, we transform this cell
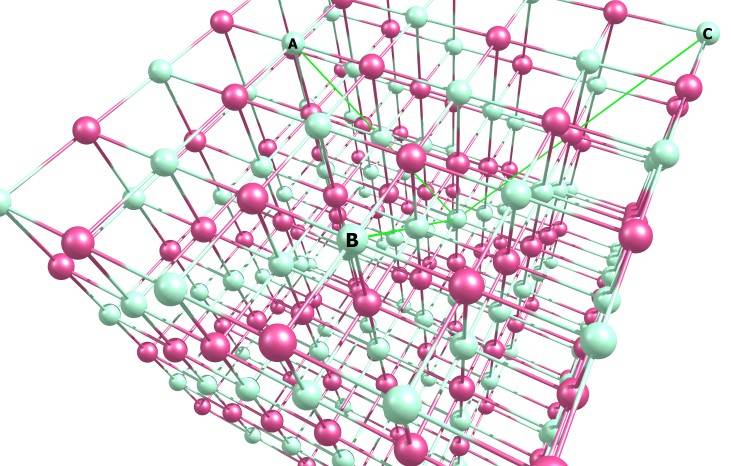
Into this cell
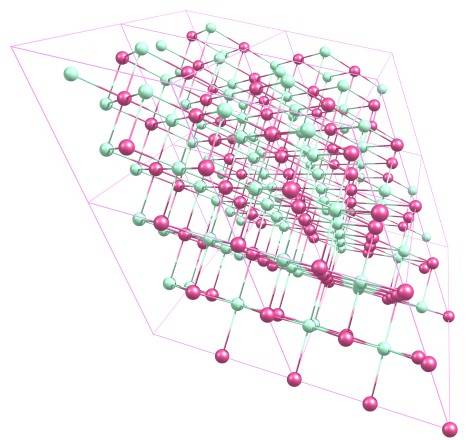
Is this correct? And is it correct that the A and B vectors are not orthogonal to each other (though they are orthogonal to C)?
PBCs mean that the atoms with e.g. fractional coordinates (0.0;0.0;0.0) and (1.0;0.0;0.0) are equivalent. PBCs in crystals are specified by three lattice vectors A, B, C; e.g. for NaCl above these vectors are three orthogonal vectors with length 5.4533 Angs each (this also mean that the crystallography parameters are: a=5.4533, b=5.4533, c=5.4533, alpha=90, beta=90, gamma=90). At the same time, for each crystal, in fact there must be an unlimited numbers of possible lattice vectors. This can be illustrated by a 2-d example:
Here the trivial PBC parameters are (1.0; 0.0) and (0.0;1.0), but also we can build the lattice vectors (3.0; -1.0) and (1.0; 3.0), which describe the same crystal.
I try to implement building the Miller indices in my program Chemcraft. Firstly the user specifies three integer numbers, e.g. 1 1 1, which mean that the new vector C will be (1.0; 1.0; 1.0) in fractional coordinates. My question is, how to build the A and B vectors if we know C. This is similar to the 2d task above, but evidently more difficult.
As far as I understand, the A and B vectors can be built in different ways; they must be orthogonal to C, maybe to each other too, but they still can be rotated along the C vector. And they must be still integers, if I understand correctly, and they must define the same crystal as it was. This can be illustrated by the 2d picture above – if the first lattice vector A=(3.0; -1.0), the second can be only B=(1.0; 3.0) to keep the same crystal.
So how can these integers A and B (3 digits for each) be obtained, if we know C?
The new values of A, B, C in terms of old (9 numbers) can be entered in the window “Redefine lattice” in Materials Studio program, I have implemented the same in Chemcraft. I suppose, to build the Miller index 1 1 1, we should specify these lattice redefinition parameters:
A: 0 1 -1
B: -1 1 0
C: 1 1 1
With these parameters, we transform this cell
Into this cell
Is this correct? And is it correct that the A and B vectors are not orthogonal to each other (though they are orthogonal to C)?