Minimize Sum of Line Segments Length w/ Point P on Line AD - Yahoo Answers

[MarkFL]

Here is the question:

CALCULUS!? A point P needs to be located somewhere on the line AD so that the total...?

Pplease help me with this question, I don't understand how to get an answer :(

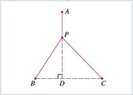
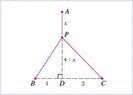
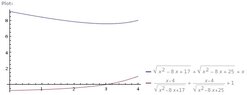
A point P needs to be located somewhere on the line AD so that the total length L of cables linking P to the points A, B, and C is minimized (see the figure). Express L as a function of x = |AP| and use the graphs of L and dL/dx to estimate the minimum value of L. (Round your answer to two decimal places. Assume that |BD| = 1 m, |CD| = 3 m, and |AD| = 4 m.)

View attachment 1718

I have posted a link there to this thread so the OP can see my work.

 

[MarkFL]

Hello realsf,

First, we may define:

$$L=\overline{AP}+\overline{BP}+\overline{CP}$$

Next, let's label the diagram with the given information:

View attachment 1719

We are given:

$$\overline{AP}=x$$

And by Pythagoras, we find:

$$\overline{BP}=\sqrt{1^2+(4-x)^2}=\sqrt{x^2-8x+17}$$

$$\overline{CP}=\sqrt{3^2+(4-x)^2}=\sqrt{x^2-8x+25}$$

Hence, we may give $L$ as a function of $x$ as follows:

$$L(x)=x+\sqrt{x^2-8x+17}+\sqrt{x^2-8x+25}$$

Differentiating with respect to $x$, we obtain:

$$\frac{dL}{dx}=1+\frac{2x-8}{2\sqrt{x^2-8x+17}}+\frac{2x-8}{2\sqrt{x^2-8x+25}}=1+\frac{x-4}{\sqrt{x^2-8x+17}}+\frac{x-4}{\sqrt{x^2-8x+25}}$$

Observing we must have $0\le x\le 4$, here are the plots of $L(x)$ and $$\frac{dL}{dx}$$ on the relevant domain:

View attachment 1720

Using a numeric root finding technique intrinsic to the CAS, we obtain:

View attachment 1721

Hence, we find:

$$L_{\min}\approx7.58$$