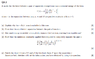Shomari
- 3
- 0
Homework Statement
Part (d) is the bit I am having trouble doing (the question is in the attachment).
Homework Equations
Apart from what is shown, I also have to use F = dV(r) / dr
The Attempt at a Solution
For Part (b), I showed this by differentiating the potential energy and equating this differential to zero. From there I rearranged the equation and solved for r.
For Part (c), I had a = r and formed the equation Vmax(r) = A*((1/m) - 1), and stated this as being the energy required to pull the two oppositely-charged ions apart.
For Part (d), I stated that the Force applied = Vmax(r) / Distance of separation, in order to find the Distance of separation I equated the potential energy to zero (where there would be zero potential energy between the two ions) and tried to solve for d. However, in doing so I got:
d = exp{[(m-1)/(m+1)]*ln(a/m)}
as the Distance of separation. I feel like this is the wrong way to answering the question, but I am unsure where I went wrong.