Mistake in Exercises for the Feynman Lectures?

In summary, the discussion addresses errors found in the exercises accompanying the Feynman Lectures on Physics. It emphasizes the importance of identifying and correcting these mistakes to enhance the educational value of the lectures and ensure accurate understanding of the concepts presented by Richard Feynman. The conversation highlights specific examples of mistakes and suggests that addressing these issues can improve the learning experience for students and readers alike.
  • #1
suh112
4
4
Homework Statement
This is problem 14.1 from "Exercises for the Feynman Lectures on Physics":

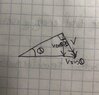
14.1 A rigid wheel of radius R is rolling without slipping on a horizontal surface. The plane of the wheel is vertical, and the axis of the wheel is moving horizontally with a speed V relative to the surface. If the axis of the wheel is parallel to the z-axis, V is in the positive x-direction, and ##\theta## the angle through which the wheel has rotated since a certain point P on the rim was in contact with the ground, show that the instantaneous velocity (speed and direction) of the point P is given by
v = V ((1- cos##\theta##)i + (sin ##\theta##) j).
Relevant Equations
v = V ((1- cos##\theta##)i + (sin ##\theta##) j)
It seems to me that the answer should be v = V((1+sinθ)i -(cosθ)j) intuitively since ##V_x## should be zero at θ = −π\2 and should be greatest when the angle is 90 degrees. Similarly, the component of velocity in the y direction should be greatest when the angle ##\theta## is 180 degrees and zero when ##\theta## is 0 degrees. Am I doing something wrong?
 

Attachments

  • IMG_1061.jpg
    IMG_1061.jpg
    44.8 KB · Views: 42
Last edited:
Physics news on Phys.org
  • #2
According to the statement of the question, angle θ is "the angle through which the wheel has rotated since a certain point P on the rim was in contact with the ground". If the wheel rolls without slipping what is the speed of certain point P on the rim relative to the point of contact with the ground? Does the given expression predict that? Does your expression predict that?
 
  • Like
Likes SammyS and Orodruin
  • #3
kuruman said:
According to the statement of the question, angle θ is "the angle through which the wheel has rotated since a certain point P on the rim was in contact with the ground". If the wheel rolls without slipping what is the speed of certain point P on the rim relative to the point of contact with the ground? Does the given expression predict that? Does your expression predict that?
Oh I misread the question. This makes sense thanks.
 
  • Like
Likes berkeman and kuruman

FAQ: Mistake in Exercises for the Feynman Lectures?

What is the nature of the mistakes found in the exercises for the Feynman Lectures?

The mistakes in the exercises for the Feynman Lectures typically include typographical errors, incorrect numerical values, ambiguities in problem statements, and occasional conceptual errors. These can lead to confusion or incorrect solutions if not identified and corrected.

Are there official errata available for the exercises in the Feynman Lectures?

Yes, there are official errata available for the Feynman Lectures, including the exercises. These errata have been compiled and corrected by various contributors over the years and can often be found on websites dedicated to the Feynman Lectures or through academic institutions that use the lectures as part of their curriculum.

How can I identify if a problem in the exercises contains a mistake?

Identifying mistakes in the exercises can be challenging. One effective approach is to cross-reference your solutions with those provided in reliable solution manuals or errata lists. Additionally, discussing the problem with peers or instructors can help clarify whether a mistake exists. If a solution seems unreasonable or inconsistent with the principles taught in the lectures, it may indicate a mistake in the problem.

What should I do if I find a mistake in the exercises for the Feynman Lectures?

If you find a mistake in the exercises, it is helpful to document it and report it to a relevant authority, such as your instructor or the publisher. Sharing your findings with the academic community through forums or dedicated websites can also help others who might encounter the same issue. Providing a clear explanation and any supporting calculations can facilitate the correction process.

Can mistakes in the exercises affect my understanding of the concepts taught in the Feynman Lectures?

While mistakes in the exercises can be frustrating, they do not necessarily undermine the overall understanding of the concepts taught in the Feynman Lectures. It is important to approach each problem critically and use mistakes as learning opportunities to deepen your comprehension. Engaging with the material, seeking clarification, and consulting additional resources can help mitigate any negative impact on your learning experience.

Similar threads

Brownian Ratchet (exercise framed by Feynman's Lectures, l. 46)
Replies
32
Views
2K
Firing mortar and cliff edge, Feynman Lectures 4.17
Replies
4
Views
2K
Complementary resources to Feynman Lectures
Replies
11
Views
1K
Calculate electric force using Coulomb's law (vector components are the struggle)
Replies
3
Views
588
Feynman Lectures on Physics - Rotation in 2 dimensions
Replies
4
Views
2K
Oblique soccer shot calculation task
2
Replies
38
Views
3K
Modeling a mass falling from one side of the Earth to the other
Replies
1
Views
587
Projectile hitting the incline plane horizontally
Replies
7
Views
4K
The height of a dielectric material between two coaxial pipes
Replies
4
Views
1K
I How Feynman proves momentum is conserved in this example?
Replies
2
Views
870

Hot Threads

Recent Insights

Back
Top