Master1022
- 590
- 116
- Homework Statement
- Why is the number of cells in the radius ## D ## determined by ## N_c = D_R^2 ## where ## D_R = \sqrt{i^2 + j^2 + ij} ##
- Relevant Equations
- area
Hi,
I was looking at some notes and trying to understand the following statement which refers to the diagram below.
"The number of cells in the radius ## D ## determined by ## N_c = D_R^2 ## where ## D_R = \sqrt{i^2 + j^2 + ij} ##
where ## i## and ##j## are the number of cells along the ## u ## and ## v ## axes respectively.
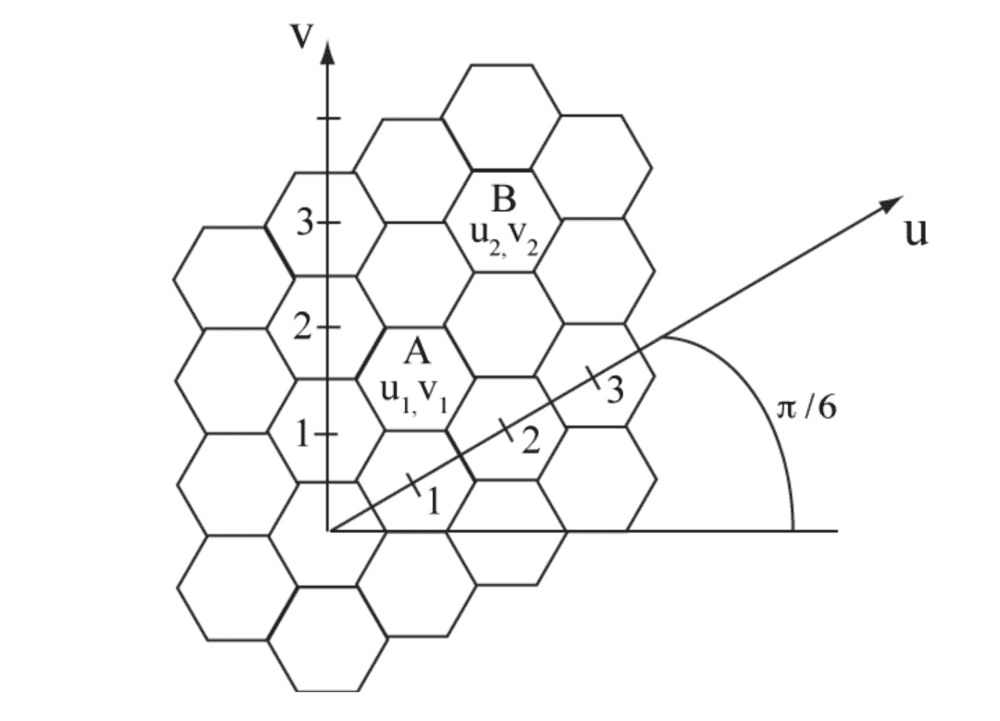
From what I understand, B is at (2, 2) in (u, v) coordinates and radius ##D## is ## = \sqrt{2^2 + 2^2 + (2)(2)} \cdot R \sqrt{3} ##. Therefore, the number of cells within the radius ## D ## should be ## 12 ##. I cannot see how this is the case, no matter how I try to encircle cells...
I think I am missing something quite simple. Any help would be greatly appreciated.
I was looking at some notes and trying to understand the following statement which refers to the diagram below.
"The number of cells in the radius ## D ## determined by ## N_c = D_R^2 ## where ## D_R = \sqrt{i^2 + j^2 + ij} ##
where ## i## and ##j## are the number of cells along the ## u ## and ## v ## axes respectively.
From what I understand, B is at (2, 2) in (u, v) coordinates and radius ##D## is ## = \sqrt{2^2 + 2^2 + (2)(2)} \cdot R \sqrt{3} ##. Therefore, the number of cells within the radius ## D ## should be ## 12 ##. I cannot see how this is the case, no matter how I try to encircle cells...
I think I am missing something quite simple. Any help would be greatly appreciated.