Intro to Power Systems: Calculating Power

[SumDood_]

Homework Statement

Calculate the power in the given circuit

Relevant Equations

P=IV

Help me understand what I am missing. So this is the circuit:

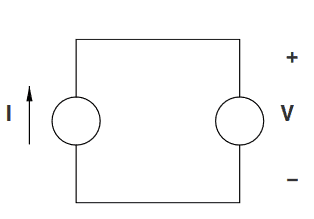
Given:
$V_{RMS} = 120V$
$I_{RMS}= 10A$
$v=Re \{Ve^{jwt}\}$
$i=Re \{Ie^{j(wt-\psi)}\}$
(a) Calculate and sketch real and reactive power P and Q as a function of the angle ψ
(b) Calculate and sketch the instantaneous power

What I've done so far:
$V = 120\sqrt{2}cos(\omega t)$
$I = 10\sqrt{2}cos(\omega t-\psi)$
$\begin{align*} P = iv &= 120\sqrt{2}cos(\omega t) \cdot 10\sqrt{2}cos(\omega t-\psi) \\ &= 120\sqrt{2}\frac{1}{2}(e^{j\omega t}+e^{-j\omega t}) \cdot 10\sqrt{2}\frac{1}{2}(e^{j(\omega t-\psi)}+e^{-j(\omega t-\psi)}) \\ &= 600(e^{j\psi} + e^{-j\psi} + e^{j(2\omega t - \psi)} + e^{-j(2\omega t - \psi)}) \\ &= 2400(cos(2\omega t - \psi) + cos(\psi)) \end{align*}$

I am not sure if the work I've done is correct. If it is, I don't understand how to differentiate P and Q from the solution I have worked out.
Any help is appreciated!

 

[scottdave]

First, which device is delivering power and which is receiving?
Then I would approach this using phsor notation.

 

[Steve4Physics]

My knowledge of EE is a bit basic but shouldn't your circuit contain a load (R and/or L and/or C)? Does it make sense to consider a circuit consisting of only an ideal current source and an ideal voltage source? Or are the sources non-ideal and you have [edit - that should be 'haven't'] supplied all the data?

 

[SumDood_]

First, which device is delivering power and which is receiving?
Then I would approach this using phsor notation.

What I have provided is what is mentioned in the question. Let's assume that the current source is delivering power.

 

[SumDood_]

My knowledge of EE is a bit basic but shouldn't your circuit contain a load (R and/or L and/or C)? Does it make sense to consider a circuit consisting of only an ideal current source and an ideal voltage source? Or are the sources non-ideal and you have suppled all the data?

You are right that this kind of circuit won't exist in the real world, but the question I've described is as stated in the book.

 

[Averagesupernova]

With the current direction shown, the voltage source (I assume) shown as DC, and the text giving a voltage in RMS (which implies AC), just how much more confusing could it get?

 

[SumDood_]

It seems that everyone is finding this question to be weird. So, I'll post the solution that is at the end of the book:
$P = \frac{1}{2}VIcos(\psi)$
$Q = \frac{1}{2}VIsin(\psi)$
Instantaneous power
$p=2Pcos^{2}(\omega t)+Qsin(2\omega t)$

 

[Steve4Physics]

It seems that everyone is finding this question to be weird. So, I'll post the solution that is at the end of the book:
$P = \frac{1}{2}VIcos(\psi)$
$Q = \frac{1}{2}VIsin(\psi)$
Instantaneous power
$p=2Pcos^{2}(\omega t)+Qsin(2\omega t)$

I suppose you can just treat the question as a maths exercise and ignore the (unphysical!) physics.

Working backwards from the expected answers gives some clues.

The complex power, $S$, is $S= P+jQ$ where $P$ is the required real power and $Q$ is the required reactive power. So you need to find a (complex) expression for $S$.

According to Wikipedia (https://en.wikipedia.org/wiki/AC_power) the complex power, $S$, is given by $S = \hat V \hat I^*$ where (in this question) $\hat V = V_{rms}e^{j \omega t}$ and $\hat I = I_{rms}e^{j(\omega t- \phi)}$. Note the use of the complex conjugate.

To get the instantaneous power I guess one way is to evaluate $p(t) = v(i)i(t)$ with $v(t) = V\cos (\omega t)$ and $i(t) = I \cos(\omega t - \phi)$ and use some trig’ identities, and the expressions for $P$ and$Q$, to get the answer in the required format.