Ben9622111222
- 31
- 0
Hi,
I am trying to mathematically model the rotation of a rotary flexible beam. There are numerous papers which study this topic but all of them are considering the beam as a fixed-free one. My case is different.

This is the beam I am trying to model. The motor axis is at the square portion towarsd the right end of the beam. The part marked in gold is the counter weight so that motor can be given low current when system is at rest.
I have tested the modes of vibration and found that it shows the nature of a free-free beam upto third mode, but for higher modes it was not clear. Only if I know how the beam behaves, can I go futher with the modeling.
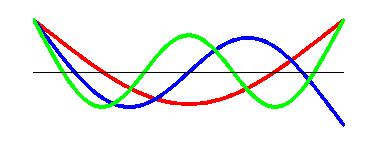
Also one node was always at the motor axis position.
Can anyone suggest me how I should go forward to understand the beam model and mathematically model it.
Thanks.
I am trying to mathematically model the rotation of a rotary flexible beam. There are numerous papers which study this topic but all of them are considering the beam as a fixed-free one. My case is different.
This is the beam I am trying to model. The motor axis is at the square portion towarsd the right end of the beam. The part marked in gold is the counter weight so that motor can be given low current when system is at rest.
I have tested the modes of vibration and found that it shows the nature of a free-free beam upto third mode, but for higher modes it was not clear. Only if I know how the beam behaves, can I go futher with the modeling.
Also one node was always at the motor axis position.
Can anyone suggest me how I should go forward to understand the beam model and mathematically model it.
Thanks.