- #1
kaspis245
- 189
- 1
- Homework Statement
- A proton with velocity ##v## is fired from infinity in the direction of another free and stationary proton as shown in the picture. Find the minimum distance between the protons.
- Relevant Equations
- Coulomb's law: ##F=\frac{1}{4πε_ο}\frac{q^2}{r^2}##
The image given with the problem:
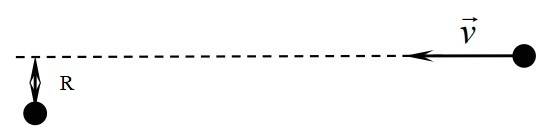
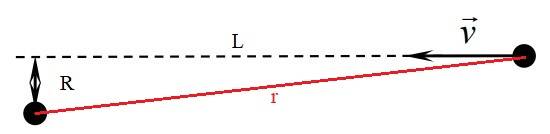
I found the original problem too difficult to solve, so I thought I'd make it easier by first considering the stationary proton as fixed in place. However, this too proved to be way more difficult than I expected. Here's the updated diagram I used in my attempt to solve it:
I started by writing the force felt by the moving proton at all times:
$$\mathbf F = \frac{1}{4πε_ο}\frac{q^2}{r^2} \hat {\mathbf r}=\frac{1}{4πε_ο}\frac{q^2}{r^3}(L\hat {\mathbf x}+R\hat {\mathbf y})$$
From this point forward I'm struggling to find any conservation law or point of equilibrium that I could use. I know that conservation of momentum yields
$$\Delta p = -mv \hat {\mathbf x} + \int \mathbf F \, dt $$
unfortunately, I don't see how's that possible to solve or how does that even help me to arrive at the solution.
Does anybody have any ideas?
I found the original problem too difficult to solve, so I thought I'd make it easier by first considering the stationary proton as fixed in place. However, this too proved to be way more difficult than I expected. Here's the updated diagram I used in my attempt to solve it:
I started by writing the force felt by the moving proton at all times:
$$\mathbf F = \frac{1}{4πε_ο}\frac{q^2}{r^2} \hat {\mathbf r}=\frac{1}{4πε_ο}\frac{q^2}{r^3}(L\hat {\mathbf x}+R\hat {\mathbf y})$$
From this point forward I'm struggling to find any conservation law or point of equilibrium that I could use. I know that conservation of momentum yields
$$\Delta p = -mv \hat {\mathbf x} + \int \mathbf F \, dt $$
unfortunately, I don't see how's that possible to solve or how does that even help me to arrive at the solution.
Does anybody have any ideas?
Last edited by a moderator: