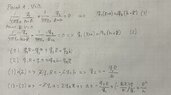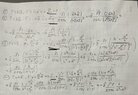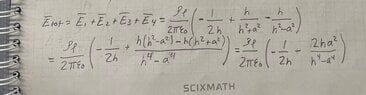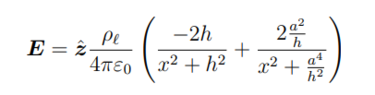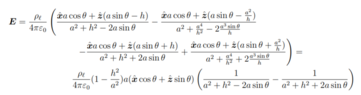Method of Images from an earthed half cylinder and plane

[JoelKTH]

Homework Statement

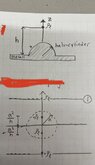
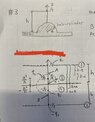
Given a linecharge $p_l$ straight across a half-cylinder on a large ground plane, as shown in figure. Determine the magnitude and direction of the force on the line charge per unit length. Also verify that the dimension of the expression is correct. The half-cylinder and the ground plane are both metal and are treated as perfectly conducting

Relevant Equations

To get the Electric field $d\mathbf{E} = \frac{dq'}{4\pi\epsilon_0}\frac{\mathbf{r} - \mathbf{r}'}{\left|\mathbf{r} - \mathbf{r}'\right|^3}$

Lorentz law $\mathbf{F} = q\mathbf{E}$

Hi,

I want to solve the problem by method of mirroring and by using the electric field by doing superposition and then adding them up to use in Lorentz law to get the force. I have attached a figure that represents the problem.

How do I know from the figure that $-p_l$ is from the half-cylinder and why is it on the positive part of z-axis? The mirroring have opposite direction of $p_l$ depending if its from the linecharge or from the metal half cylinder.

How do I know that the $-p_l$ is on the distance $z=\frac{a^2}{h}$?

How should I pick my source and field vectors? I believe I should have my field vector as $r = h \hat{\mathbf{z}}$.

Kind regards,

 

[haruspex]

Your first figure shows the line charge as a short horizontal line of unstated length, terminating above the middle of the half cylinder. Your second looks like it is an infinite line both ways.
Can you calculate the potential at the top of the half cylinder?

 

[JoelKTH]

Your first figure shows the line charge as a short horizontal line of unstated length, terminating above the middle of the half cylinder. Your second looks like it is an infinite line both ways.
Can you calculate the potential at the top of the half cylinder?

I actually solved it by knowing that V=0 both at the top of the cylinder and the bottom. I used two equations by adding R to the figure.

 

[JoelKTH]

I managed to get the same answer as my professor, however we defined the charges differently.
Am I free to choose both alternative A and B(see figure attached) or is one of them to prefer?

 

[JoelKTH]

I was a bit confused when to use what equation. From my calculations i used $E =\frac{\rho_l}{2\pi\epsilon_0} \frac{(r-r')}{|r-r'|^3}$ and got the correct result. I don't quite get why this equation is to be used compared to my first instinct:

$dE =\frac{dq}{4\pi\epsilon_0} \frac{(r-r')}{|r-r'|^3}$,
$dq= \rho_l dr$ --> $E= \frac{\rho_l}{4\pi\epsilon_0} \int \frac{(r-r')}{|r-r'|^3} dr$

How can I know which one to use?

 

[JoelKTH]

Here are my calculations and answer:

 

[JoelKTH]

Then I did dimensionanalysis and its ok. But I noticed that one needs to check the boundary conditions.
My professor writes in the solution:
To convince ourselves that the charge distribution is correct, lets examine the boundary condition. First, let z = 0. The symmetry in the choice of the line charge implies that at $r = x\hat{x}$, we obtain (see attached figure). That means z=0 is normal to the Electric field on the plane.

I am a bit lost what is happening here. Because now my professor has used the formula that I thought I was not supposed to use.
He continues to use it to examine the semicircle: we note that on the surface of the cylinder, we have r = $\hat{x}a \cos \theta + \hat{z}a \sin \theta$(see second attached figure).
Then, since $\hat{x}\cos\theta + \hat{z}\sin\theta$ is normal to the cylinder (parallel to r), the electric field satisfies the normal condition to the surface, and E is the unique solution.

Making me very confused.

 

[haruspex]

I managed to get the same answer as my professor, however we defined the charges differently.
Am I free to choose both alternative A and B(see figure attached) or is one of them to prefer?

A is not going to give a zero potential over the top of the dome.