Module Over a Division Ring - Blyth Theorem 1.1, Part 4

[Math Amateur]

I am reading T. S. Blyth's book "Module Theory: An Approach to Linear Algebra" ... ... and am currently focussed on Chapter 1: Modules, Vector Spaces and Algebras ... ...

I need help with an aspect of Theorem 1.1 part 4 ...

Theorem 1.1 in Blyth reads as follows:

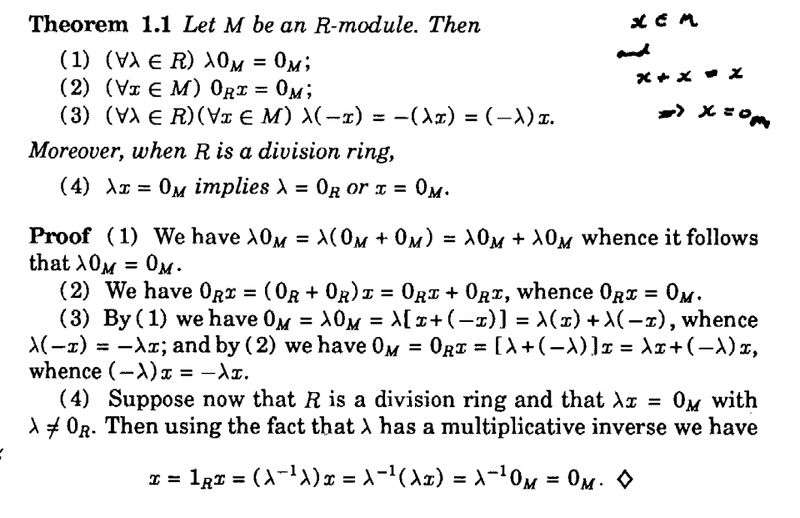
In the above text, in part 4 of the Theorem we read:" ... ... when $R$ is a division ring

(4) $\lambda x = 0_M$ implies $\lambda = 0_R$ or $x = 0_M$ ... ... "Blyth proves that if $R$ is a division ring and $\lambda x = 0_M$ with $\lambda \neq 0_R$ then we have that $x = 0_M$ ... ...But ... ... Blyth does not show that if $R$ is a division ring and $\lambda x = 0_M$ with $x \neq 0_M$ then we have that $\lambda = 0_R$ ... ...Can someone please help me to prove this ...

Peter

 

[micromass]

Contrapositive.

 

[Math Amateur]

Contrapositive.

Sorry Micromass ... I do not follow you ...

Can you explain what you mean more explicitly ... ?

My apologies for not following you ...

Peter

 

[micromass]

https://en.wikipedia.org/wiki/Contraposition

 

[Math Amateur]

https://en.wikipedia.org/wiki/Contraposition

Hi Micromass ... I understand the meaning of "contrapositive" ... but fail to see exactly how it applies to the problem that I posed ...

Peter

 

[Math Amateur]

Hi Micromass ... I understand the meaning of "contrapositive" ... but fail to see exactly how it applies to the problem that I posed ...

Can you be more explicit in what you mean regarding the specific problem ...

Peter

 

[micromass]

Come on, think a bit about it. You answered merely 6 minutes after me. I'm not here to spoonfeed you the answer.

 

[fresh_42]

Proof of (4).
Case 1: $\lambda = 0_R$ $\checkmark$ by (2)
Case 2: $\lambda \neq 0_R$ - see Blyth's proof

 

[Math Amateur]

Proof of (4).
Case 1: $\lambda = 0_R$ $\checkmark$ by (2)
Case 2: $\lambda \neq 0_R$ - see Blyth's proof

Well ... thanks fresh_42 ... that is an easy resolution to the issue ...

BUT ... still reflecting and wondering about Case 1 ...

... indeed ... does $( 0_R x = 0_M )$ ...

... imply (or mean) that ...

$( \lambda x = 0_M \text{ and } x \neq 0_M \Longrightarrow \lambda 0_R )$

is true ...But why exactly ... ?(Not quite sure why this logic bothers me ...)

Peter

 

[Math Amateur]

Thanks for th

Well ... thanks fresh_42 ... that is an easy resolution to the issue ...

BUT ... still reflecting and wondering about Case 1 ...

... indeed ... does $( 0_R x = 0_M )$ ...

... imply (or mean) that ...

$( \lambda x = 0_M \text{ and } x \neq 0_M \Longrightarrow \lambda 0_R )$

is true ...But why exactly ... ?(Not quite sure why this logic bothers me ...)

Peter

Contrapositive.

Contrapositive.

Thanks for the hint, micromass ...

in (4) Blyth has shown the following:

$( \lambda x = 0_M \text{ and } \lambda \neq 0_R ) \longrightarrow (x = 0_M)$ ... ... ... (1)

So ... contrapositive of (1) is as follows:

$\neg ( x = 0_M) \longrightarrow \neg ( \lambda x = 0_M \text{ and } \lambda \neq 0_R )$

But ... how do I progress from here ...

Can someone help further ...?

Peter

 

[fresh_42]

We have $\lambda x = 0_M$ as a fact.
(2) is needed to show that $\lambda = 0_R$ is a solution at all.
Since there are only the two possibilities for $\lambda$ - either being zero or not - and the first solves the condition according to (2), it is sufficient to consider the other case, $\lambda \neq 0_R$.

You may write the whole thing as:

$[\lambda x = 0_M]$
$= \; (\lambda x = 0_M) \, ∧ \, \text{ (true) }$
$= \; (\lambda x = 0_M) \, ∧ \, [(\lambda = 0_R)\, ∨ \, (\lambda \neq 0_R)]$
$= \; [(\lambda x = 0_M) \, ∧ \, (\lambda = 0_R)] \, ∨ \, [(\lambda x = 0_M) \, ∧ \, (\lambda \neq 0_R)]$

→ (now I use (2), i.e. if $\lambda = 0_R$ is true then $\lambda x = 0_M$ is also true)

$= \; (\lambda = 0_R)\, ∨ \, [(\lambda x = 0_M) \, ∧ \, (\lambda \neq 0_R)]$

Therefore if $(\lambda = 0_R) = \text{ (true) }$ we are done and we may ask when $[(\lambda x = 0_M) \, ∧ \, (\lambda \neq 0_R)]$ will be true without $(\lambda = 0_R)$ being true, i.e. $(\lambda \neq 0_R)$. Now Blyth has shown

$$[(\lambda x = 0_M) = \text{ (true) }] \,⇔\, [(\lambda = 0_R)=\text{ (true) }]\, ∨ \, [((\lambda x = 0_M) \, ∧ \, (\lambda \neq 0_R)) \,=\, \text{ (true) }]\, \overset{Blyth}⇒\, [(\lambda = 0_R)=\text{ (true) }]\, ∨ \, \; [(x=0_M) \,=\, \text{ (true) }]$$

 

[Math Amateur]

Thanks for that fresh_42 ... most helpful ...

Much appreciate your assistance ...

Peter