Molecules when Born-Oppenheimer approximation doesn't work

[BillKet]

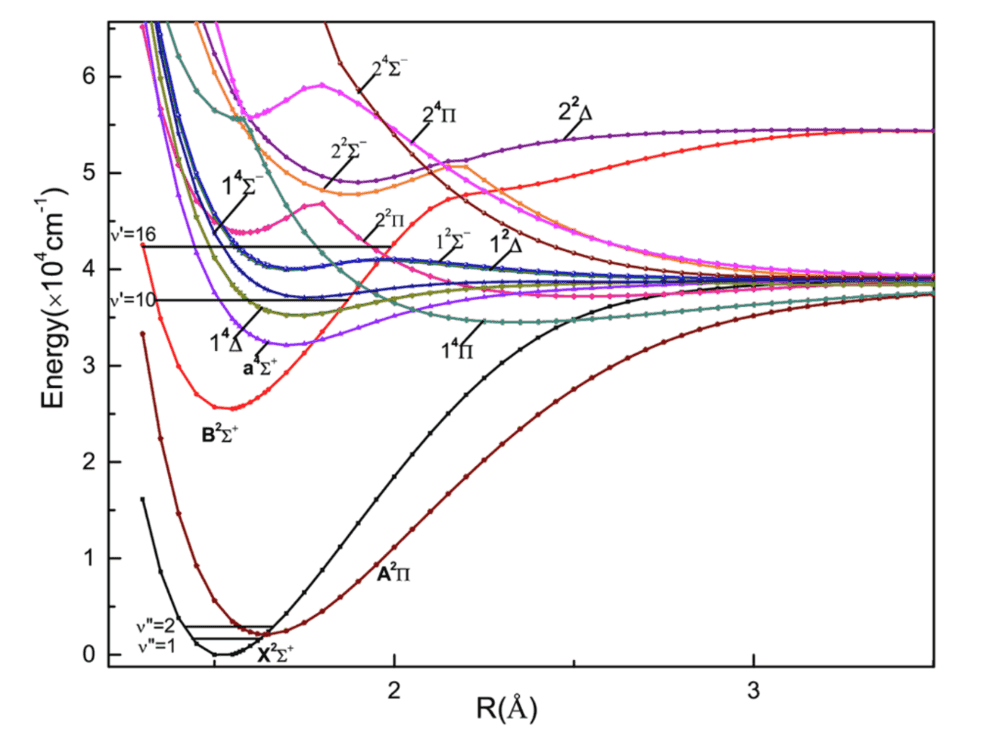
Hello! I am trying to do some molecular physics calculations, involving the calculation of the expectation value of certain vector operators (such as the electric dipole moment of the molecule) in given molecular states. In most cases assuming the Born-Oppenheimer (or adiabatic) approximation makes things easier, as I can separate the rotating frame of the molecule from the lab frame and some terms can be calculated analytically while others are taken from measurements or numerical calculations. However my (limited) experience with these calculations (and basically all the books and papers I read) assumed the Born-Oppenheimer approximation. However now I need to do some calculations in a system whose energy levels look like in the figure below. As you can see the ground state ($X^2\Sigma^+)$, which is what I care about, is very close in energy to the first excited state ($A^2\Pi$). From what I read, the Born-Oppenheimer approximation holds well when the electronic level of interest is separated from the others (so that the higher order corrections going like $1/\Delta E$ are very small). However in our case that is not really the case, so I am not sure I can just use the techniques that I would normally use and I don't really know what to do. Can someone point me towards some books or papers that actually describe this situation? Thank you!

 

[DrDu]

The electronic states are of different symmetry. Hence if you use these diabatic states transitions are negligible.

 

[BillKet]

The electronic states are of different symmetry. Hence if you use these diabatic states transitions are negligible.

Thank you for your reply! Could you please elaborate a bit, as I am not really sure I understand what you mean. What symmetry are you referring to? I attached below a screen shot from Molecular Physics by Demtroder. As far as I understand, the first term would give the Born-Oppenheimer energies, the second term would account for the adiabatic approximation, while the 3rd (and higher) would contribute to the non-adiabatic part. Here $\phi_n$ are the Born-Oppenheimer electronic wavefunctions. So in my case, the denominator in equation 2.26 is small (at least compared to what I was used to work with before). Are you saying that because of some symmetry arguments, the numerator is zero? (The $W_{nk}$ is the expectation value of the nuclear kinetic energy between 2 electronic states). I am not sure I see what that is the case. Thank you!

 

[DrDu]

Sorry, I was only with my cell phone.
Maybe you want to have a look at Landau Lifshetz, Quantum Mechanics (Vol III). They give a very nice discussion of linear molecules.
The symmetry group I was referring to is $C_{\infty v}$ and the symmetry labels of the representations are $\Sigma^+$, $\Pi$, $\Delta$ ... It is easy to see that the lowest two states are of different symmetry. As the potential energy surfaces cross, they aren't BO-surfaces, i.e. you are right in that the BO-approximation breaks down. The BO- surfaces would be the lower "w" and the upper "v" shaped surfaces. Clearly such a description would be unnatural, here. Furthermore, as the w and v shaped surfaces touch, the non-adiabatic coupling $W_{nk}$ would diverge at that point. This can be avoided considering the crossing "diabatic" surfaces instead, which are of different symmetry so that all matrix elements between these states vanish.

 

[BillKet]

Sorry, I was only with my cell phone.
Maybe you want to have a look at Landau Lifshetz, Quantum Mechanics (Vol III). They give a very nice discussion of linear molecules.
The symmetry group I was referring to is $C_{\infty v}$ and the symmetry labels of the representations are $\Sigma^+$, $\Pi$, $\Delta$ ... It is easy to see that the lowest two states are of different symmetry. As the potential energy surfaces cross, they aren't BO-surfaces, i.e. you are right in that the BO-approximation breaks down. The BO- surfaces would be the lower "w" and the upper "v" shaped surfaces. Clearly such a description would be unnatural, here. Furthermore, as the w and v shaped surfaces touch, the non-adiabatic coupling $W_{nk}$ would diverge at that point. This can be avoided considering the crossing "diabatic" surfaces instead, which are of different symmetry so that all matrix elements between these states vanish.

Thank you so much for the reply, and I am sorry for my delayed reply. I am quite new to this field and I am still not 100% I understand this. From what I read, in BO approximation (in which you get adiabatic potential energy curves (PEC)) we ignore the off diagonal matrix elements of the nuclear kinetic energy term. However if we have an avoided crossing, such that 2 adiabatic surfaces come very close together, we can't ignore that, so we do a unitary transformation going to the diabatic representation. So is the difference between the 2 approaches just in the way we choose the electronic wavefunction basis, such that the corresponding hamiltonian dominates over the perturbations? Also in general in a PEC, how do I know if the curves are in the adiabatic representation or not, assuming they don't cross? And how do I approach vibrational energies? In the example above, if I add more vibrational energy to the $X^2\Sigma^+$ state, would I just go higher and higher until I reach the dissociation energy of that electronic state, or will I jump to the $A^2\Pi$ state if that is more energy favorable? Finally, when going to the rotational levels (and this is actually the most related to my original question about the calculations I need to do), do I choose a Hund case based on the diabatic state I am in (here I am talking about some analytical calculations, assuming Hund cases hold, not fully numerical ones), so for example, for the ground state I would assume (most probably) a Hund case b? Or do I need to write it as a linear combination of Hund cases a (most probably) and b, due to the intersection with the $A^2\Pi$ state? I am sorry for the long post.

 

[DrDu]

So is the difference between the 2 approaches just in the way we choose the electronic wavefunction basis, such that the corresponding hamiltonian dominates over the perturbations?

Yes

Also in general in a PEC, how do I know if the curves are in the adiabatic representation or not, assuming they don't cross?

If the two curves do not get really near to each other at one point, the adiabatic representation is much better than the diabatic one.

And how do I approach vibrational energies? In the example above, if I add more vibrational energy to the $X^2\Sigma^+$ state, would I just go higher and higher until I reach the dissociation energy of that electronic state, ...

Yes, this is what is happening.

Finally, when going to the rotational levels (and this is actually the most related to my original question about the calculations I need to do), do I choose a Hund case based on the diabatic state I am in (here I am talking about some analytical calculations, assuming Hund cases hold, not fully numerical ones), so for example, for the ground state I would assume (most probably) a Hund case b?

Yes, use the Hund cases according to the symmetry label of the diabatic states to discuss the Hund cases.

Concerning the vibrational levels: I don't know whether your molecule is diatomic or multiatomic.
In the latter case, there will be bending modes of the molecule which will break the rotational symmetry so that the degeneracy of the electronic states gets lifted in the bent states and the diabatic couplings cannot be assumed to vanish. This is called Renner-Teller effect.

Concerning the rotational energy levels, there is a somewhat similar effect called lambda doubling.

Cheers!

 

[BillKet]

Yes

If the two curves do not get really near to each other at one point, the adiabatic representation is much better than the diabatic one.

Yes, this is what is happening.

Yes, use the Hund cases according to the symmetry label of the diabatic states to discuss the Hund cases.

Concerning the vibrational levels: I don't know whether your molecule is diatomic or multiatomic.
In the latter case, there will be bending modes of the molecule which will break the rotational symmetry so that the degeneracy of the electronic states gets lifted in the bent states and the diabatic couplings cannot be assumed to vanish. This is called Renner-Teller effect.

Concerning the rotational energy levels, there is a somewhat similar effect called lambda doubling.

Cheers!

Thank you so much for this, it is really helpful! My molecule is diatomic (it is actually a molecular ion $SiO^+$). One thing I am still confused about, regarding Hund cases is this. Assuming we solve the Schrodinger equation for the electronic hamiltonian only, so we get adiabatic/BO eigenstates, given that in the case of a diatomic molecule we have cylindrical symmetry, the eigenstates should have a well-defined value of the projection of the electronic orbital angular momentum on the internuclear axis (the $\Lambda$ paramters). If I understand it correctly, the BO eigenstates for the lowest 2 levels above would correspond to the "w" and "v" shaped surfaces that you mentioned. So I would expect that these 2 surfaces to have a well defined value of $\Lambda$. However, the diabatic states are mixing these 2 adiabatic states. For example, the diabatic state labeled $X^2\Sigma^+$ has (according to the usual convention) $\Lambda = 0$ (and hence it is most probably in a Hund case b). How can it have a well defined $\Lambda$, given that it mixes 2 adiabatic levels with different values of $\Lambda$?

 

[DrDu]

No, it is the other way round. The diabatic states have well defined Lambda values, the BO-states not. At the crossing point - very artificially - the symmetry of the BO-states would change. This sudden change of energy level is also responsible for the diverging of the nonadiabatic coupling.

 

[BillKet]

No, it is the other way round. The diabatic states have well defined Lambda values, the BO-states not. At the crossing point - very artificially - the symmetry of the BO-states would change. This sudden change of energy level is also responsible for the diverging of the nonadiabatic coupling.

Wait, I thought that BO states are the actual eigenstates of the electronic hamiltonian (I mean for a fixed R configuration). Given that the electronic hamiltonian has cylindrical symmetry, shouldn't its eigenstates (i.e. the BO states) has a well defined $\Lambda$ value?

 

[DrDu]

They do for fixed R, but this does not guarantee that symmetry changes suddenly if you change R!

 

[BillKet]

They do for fixed R, but this does not guarantee that symmetry changes suddenly if you change R!

Sorry, but I am still confused. What do you mean by "suddenly"? Isn't the point of BO surfaces that they are formed by adjusting R very slowly i.e. in an adiabatic manner, so that if the $\Lambda$ is well defined for a given R, won't it be well defined (and the same) for all R?

 

[DrDu]

Yes, normally, you assume that the nuclei move slow enough so that if the electronic wavefunction changes smoothly with R, the electronic wavefunction has time to adjust. However, in the case we are considering, the electronic wavefunction changes suddenly at the crossing point, from a state with Sigma to Pi symmetry, in your case. Suddenly, in the sense of apruptly at one point. This can't be avoided by nuclei moving more slowly.

 

[BillKet]

Yes, normally, you assume that the nuclei move slow enough so that if the electronic wavefunction changes smoothly with R, the electronic wavefunction has time to adjust. However, in the case we are considering, the electronic wavefunction changes suddenly at the crossing point, from a state with Sigma to Pi symmetry, in your case. Suddenly, in the sense of apruptly at one point. This can't be avoided by nuclei moving more slowly.

I think I am missing something conceptually. Solving the electronic hamiltonian, has nothing to do with how close the PEC are. That comes into play later when we expand a general solution of the full Hamiltonian as a linear combination of products of electronic and nuclear states and off diagonal terms might be significant. But looking only at the electronic hamiltonian, its eigenstates are adiabatic all along the PEC. So in the case of the bottom adiabatic PEC, which has a w shape, if we reduce the R slowly from infinity, we start on the brown curve, follow the w shape and end up in the bottom of the black curve. But all this would be, by definition, adiabatic. So if we go from the brown curve to the black curve adiabatically, souldn't the $\Lambda$ be the same all along, by the definition of adiabacity? I.e. Shouldn't the left part of the black curve and the right part of the brown curve (relative to the interaction point) have the same $\Lambda$, given that you can go from one to the other using an adiabatic transformation?

 

[DrDu]

The adiabatic electronic wavefunctions are defined as those diagonalizing the electronic hamiltonian $T_\mathrm{e} +V(R)$ for each R. However, this does not guarantee that the lowest energy eigenstate has the same symmetry for different R.

 

[BillKet]

The adiabatic electronic wavefunctions are defined as those diagonalizing the electronic hamiltonian $T_\mathrm{e} +V(R)$ for each R. However, this does not guarantee that the lowest energy eigenstate has the same symmetry for different R.

Oh I see, so what you meant was that (to a rough approximation) if I move adiabatically along the w shaped, lowest energy BO PEC, I would be in a $\Lambda = 1$ state until the peak of the w, then I would suddenly switch to a $\Lambda = 0$ state. Is that right? I will look more into the math of it. What confused me (and it still does) is that I assumed that you can't have this kind of sudden changes if you adjust the system adiabatically. Basically around the peak of the w, just by bringing the nuclei slightly closer, the electron completely changes its configuration. It is still hard to visualize this, but I understand what you mean now. One more questions I have then, when the PEC are far apart, and we implicitly assume the BO approximation, how do we know that they are have the same $\Lambda$ for all R. Initially I took that for granted, as I used my wrong reasoning from above, but now it is not obvious to me anymore why we assign to a give PEC a unique value of $\Lambda$. I assume that it has to do with the presence or absence of that w shape, but I am not sure. Thank you!

 

[DrDu]

Yes, this explanation of the sudden switch at the tip of the "V" and "W" is correct, now to your question about the energy gap.
Let $|u\rangle$ and $| v\rangle$ be two electronic eigenstates of $T_e+V(R)$.
Now the important part of the nonadiabatic is $\langle V| \partial u\rangle /\partial R \partial/\partial R$.
Now, as $\langle v| u\rangle=0$, $\partial \langle v/\partial R| u\rangle =-\langle v| \partial u\rangle/\partial R$.
Furthermore, $\langle v| H_{el}| u \rangle =0$, and therefore
$0= \partial \langle v| H_{el}| u \rangle/\partial R=\partial v/\partial R|H_{el} u\rangle +\langle Hv| \partial u\rangle/\partial R+\langle v| \partial V/\partial R| u \rangle$.
Hence we get
$\langle v| \partial u\rangle /\partial R=\langle v| \partial V/\partial R | u \rangle /(E_u-E_v)$ (don't blame me for wrong signs!). This is known as the Hellmann-Feynman theorem.
The numerator is always finite, so the couplings will become large when the energy difference in the numerator becomes small. Where the energy gap between the PES is large, nonadiabatic effects won't be a problem.