Moment of force exerted by water on tube

[Vibhor]

Homework Statement

Homework Equations

Bernoulli's equation : $P + \frac{1}{2}ρv^2 + ρgh$ = constant

The Attempt at a Solution

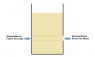
The pressure at the interface is $P_{int} = P_0 + ρgH$ .

Applying bernoulli's equation between point at the interface of two liquids and exit of the tube .

$P_{int} + ρg(\frac{H}{2}+\frac{H}{4})$ = $P_0 + \frac{1}{2}(2ρ)v^2$

$v = \frac{\sqrt{7gH}}{2}$ .

This doesn't give correct answer .

.What is the mistake ?

Thanks

 

[TSny]

Applying bernoulli's equation between point at the interface of two liquids and exit of the tube .

##P_{int} + ρg(\frac{H}{2}+\frac{H}{4}) $=$ P_0 + \frac{1}{2}(2ρ)v^2##

Did you use the correct density on the left?

 

[Vibhor]

Ok .

It should be 2ρ . It gives $v = \frac{\sqrt{5gH}}{2}$ which again seem incorrect .

 

[TSny]

It should be 2ρ . It gives $v = \frac{\sqrt{5gH}}{2}$ which again seem incorrect .

Check to see if the 2 should be inside the square root.

 

[Vibhor]

Sorry . It should be $v = \sqrt{\frac{5gH}{2}}$ . Is this the speed at which the fluid flows in the tube ?

 

[TSny]

Sorry . It should be $v = \sqrt{\frac{5gH}{2}}$ . Is this the speed at which the fluid flows in the tube ?

You calculated $v$ for a point at the exit of the tube. Can you give a reason why this is also the speed at other points inside the tube?

 

[Vibhor]

This will not be the speed at other points in the tube .

If I need to find vertical force exerted by the tube , should I be looking at speed of the fluid at the point where tube bends ?

 

[TSny]

This will not be the speed at other points in the tube .

Why not? Does the "continuity equation" tell you anything?

If I need to find vertical force exerted by the tube , should I be looking at speed of the fluid at the point where tube bends ?

Yes.

 

[Vibhor]

Why not? Does the "continuity equation" tell you anything?

Right . The speed would be same in the entire tube length = $v = \sqrt{\frac{5gH}{2}}$ .

Now calculating the vertical force exerted by fluid on the tube . For that I considered the volume of fluid in the tube i.e from the hole in the container till the exit of the tube .
The vertical forces on this parcel of fluid are F_v , force due to tube and pressure force $P_0 A$ at the exit . The rate of change of vertical momentum of fluid would be $ρAv^2$ .

Doing force balance in vertical direction ,taking upwards as positive , $P_0 A + F_v = -ρAv^2$ i.e $F_v = -ρAv^2 - P_0 A$ ??

 

[TSny]

Now calculating the vertical force exerted by fluid on the tube . For that I considered the volume of fluid in the tube i.e from the hole in the container till the exit of the tube .
The vertical forces on this parcel of fluid are F_v , force due to tube and pressure force $P_0 A$ at the exit . The rate of change of vertical momentum of fluid would be $ρAv^2$ .

Doing force balance in vertical direction ,taking upwards as positive , $P_0 A + F_v = -ρAv^2$ i.e $F_v = -ρAv^2 - P_0 A$ ??

I think that's OK, except that in the statement of the problem ρ stands for the density of the other fluid, not the density of the fluid in the tube.

 

[Vibhor]

Yes , it should be 2ρ .

But , then the moment of the force exerted by liquid will have a P₀ term whereas none of the options have P₀ ??

 

[TSny]

Yes , it should be 2ρ .

But , then the moment will have a P₀ term whereas none of the options have P₀ ??

You'll need to consider the atmospheric pressure acting on the tube over the region shown below.

 

[Vibhor]

You'll need to consider the atmospheric pressure acting on the tube over the region shown below.

But this pressure is not acting directly on the fluid ?

 

[TSny]

Right. You are ultimately interested in the net torque on the tube. (I believe this is what the problem is actually having you calculate). I will let you think about this.

 

[Vibhor]

If I consider (tube+fluid flowing through it) as system , then since the system is in vertical equilibrium , the force due to atmosphere at the top of the bend is balanced by the pressure force at the exit .

Is this a valid reason why P₀A should not appear in the expression for vertical force and $F_v = -ρAv^2$ only and not $F_v = -ρAv^2 - P_0 A$ ?

 

[Vibhor]

You are ultimately interested in the net torque on the tube. (I believe this is what the problem is actually having you calculate). I will let you think about this.

Net torque on the tube = net force on the tube in vertical direction x moment arm

net force on the tube in vertical direction = vertical force on the tube due to fluid . So , again I have come to the point whether I should use $F_v = -ρAv^2 - P_0 A$ or $F_v = -ρAv^2$ ?

In the book also , in one of the sample problems it is mentioned that vertical force due to liquid exerted on the tube = $F_v = -ρAv^2$ , but then in post#9 I have obtained that $F_v = -ρAv^2 - P_0 A$ . So which one is correct ??

Please let me know which expression for the vertical force is correct before I think about torque .

 

[TSny]

Good question. I think that they probably expect you to use just $F_v = -\rho Av^2$. If you include the term $-P_0A$, then you will get an extra upward force exerted on on the tube by the fluid of $+P_0A$. But this is canceled out by the external atmospheric pressure acting on the tube as indicated in my drawing. If I use $F_v = -\rho Av^2$ I do get one of the specific answers listed. [EDIT: $\rho$ should be $2\rho$ in these expressions.]

They also seem to be neglecting the force due to the weight of the fluid in both the horizontal and vertical sections of the tube. If I include this, then I do not get one of the specific answers. Of course, there is always (D), none of the above.

Anyway, see what you get. Hopefully, others will chime in.

 

[Vibhor]

I think that they probably expect you to use just $F_v = -\rho Av^2$

That gives option A) which is indeed the correct answer . But this expression is used everywhere , rather I should say it is used as a standard result . But I am really surprised by the omission of $P_0A$ term .I am still not convinced why the downward force on the bend as indicated in your drawing should cancel the upward $P_0A$ force .

 

[TSny]

That gives option A) which is indeed the correct answer . But this expression is used everywhere , rather I should say it is used as a standard result . But I am really surprised by the omission of $P_0A$ term .I am still not convinced why the downward force on the bend as indicated in your drawing should cancel the upward $P_0A$ force .

The $P_0A$ term that you included is a force on the fluid. Then, when you solved for the vertical force, $F_v$, that the tube exerts on the fluid, you got $F_v = -(2\rho) A v^2 - P_0A$. Thus, by the third law, the fluid exerts the same force, but upwards, on the tube. But the atmospheric pressure acting externally on the tube has an unbalanced force contribution downward (shown in my figure) that happens to equal $P_0A$. This downward force on the tube from the atmosphere cancels the part, $P_0A$, of the upward force on the tube from the fluid. So, the net effect is to just use $F_v = -(2\rho) Av^2$ and forget about the unbalanced atmospheric pressure acting on the tube. At least that's how I see it.

I'm still confused as to why we can neglect the weight of the fluid in the analysis. It seems to me that it contributes the same order of magnitude as the other forces.

 

[Vibhor]

The $P_0A$ term that you included is a force on the fluid. Then, when you solved for the vertical force, $F_v$, that the tube exerts on the fluid, you got $F_v = -(2\rho) A v^2 - P_0A$. Thus, by the third law, the fluid exerts the same force, but upwards, on the tube. But the atmospheric pressure acting externally on the tube has a an unbalanced force contribution downward (shown in my figure) that happens to equal $P_0A$. This downward force on the tube from the atmosphere cancels the part, $P_0A$, of the upward force on the tube from the fluid. So, the net effect is to just use $F_v = -(2\rho A) v^2$ and forget about the unbalanced atmospheric pressure acting on the tube. At least that's how I see it.

Nice analysis !

Considering (tube+fluid flowing through it) as system and using the fact that the system is in horizontal equilibrium , there will also be a net atmospheric pressure acting on the tube horizontally (at the bend) acting leftwards , but this will be balanced by pressure force PA at the hole of the container ??

Likewise would it be correct to say that the horizontal force exerted by fluid on the tube is $F_v = -(2\rho) A v^2 - PA$ , where $P$ is the pressure at the hole of the container but , net horizontal force on the tube will be $F_v = -(2\rho) A v^2$ ??

 

[TSny]

Considering (tube+fluid flowing through it) as system and using the fact that the system is in horizontal equilibrium , there will also be a net atmospheric pressure acting on the tube horizontally (at the bend) acting leftwards

Yes.

but this will be balanced by pressure force PA at the hole of the container ??

Well, the atmospheric force will be $P_0 A$ which will be different in magnitude from the force $PA$.

Likewise would it be correct to say that the horizontal force exerted by fluid on the tube is $F_v = -(2\rho) A v^2 - PA$ , where $P$ is the pressure at the hole of the container

I would write this with positive signs to indicate a direction to the right (and maybe a subscript h instead of v).

but , net horizontal force on the tube will be $F_v = -(2\rho) A v^2$ ??

As mentioned above, the forces $PA$ and $P_0A$ will not cancel. So, the "net" horizontal force on the tube would be $F_h = (2\rho) A v^2 +(P - P_0)A$. Since the tube remains at rest, there will actually need to be another horizontal force to balance this "net" force. This would come from the tank where the tube is attached to the tank.

 

[Vibhor]

So, the "net" horizontal force on the tube would be $F_h = (2\rho) A v^2 +(P - P_0)A$

This is net horizontal force on the tube OR horizontal force on the tube due to fluid ??

 

[TSny]

This is net horizontal force on the tube OR horizontal force on the tube due to fluid ??

It's the sum of the horizontal force on the tube due to the fluid and the horizontal force on the tube due to the atmosphere.

 

[Vibhor]

Ok .

And horizontal force on the tube due to fluid will be $(2\rho) A v^2 +PA$ ??

 

[TSny]

Ok .

And horizontal force on the tube due to fluid will be $(2\rho) A v^2 +PA$ ??

Yes, that's how I see it anyway. (Where's Chestermiller when we need him? Maybe I'll send him a note and see if he will take a look.)

 

[Vibhor]

I agree with your analysis . The problem is that it is different from what is written in almost every book or notes I have come across .

A similar confusion has occurred in the following set up . Again this a standard problem/concept in fluids .

Consider a container with fluid (density ρ) having a hole of cross section area A at the wall of the container(towards the right side), a distance h from the surface of water. The speed of fluid coming out will be √(2gh) and the reaction force exerted by fluid on the container is given by $\rho A v^2$ . This is a standard result derived in books .

Now , there will be two horizontal forces acting on the fluid , that due to container and force due to atmospheric pressure acting towards left . The horizontal rate of change of momentum will be $\rho A v^2$.

Take right direction as positive , $F_H - P_0A = \rho A v^2$ i.e $F_H = \rho A v^2 + P_0A$ . In other words the force exerted by fluid on the container is $- \rho A v^2 - P_0A$ .

In this case also I get an extra $- P_0A$ term

Again a discrepency in a standard result ??

Please help me resolve the confusion .

 

[TSny]

At least naively, I think the discrepancy is similar to before. See the figure below. The horizontal force on the fluid includes the external atmospheric pressure at the hole: $-P_0A$, as you note. This leads to your result $F_H = \rho Av^2 + P_0A$ for the horizontal force that the container exerts on the fluid. So, by the third law, the fluid exerts a horizontal force of $-\rho Av^2 - P_0A$ on the tank. But the atmosphere exerts an unbalanced force to the right of $+P_0A$ on the tank. So, the fluid and atmosphere together exert a horizontal force to the left on the tank equal to $-\rho Av^2$. Therefore, effectively, the discharge of the fluid results in an overall "reaction force" of $-\rho Av^2$ to the left. If the tank is resting on a frictionless surface, you would need to exert a horizontal force of $+\rho Av^2$ on the tank to hold it at rest.

 

[Vibhor]

Brilliant analysis . Thanks a lot . It seems that $\rho A v^2$ is not the force due to ejecting fluid on the container rather it is the net horizontal force on the container due to ejection of the fluid . Right ??

Please see the attached image .

In figure A) fluid moves through a pipe which is 3/4th part of a circle whereas in B) the fluid moves through a U tube .The tubes are at rest on a horizontal table which means there must be some support to keep them at place .The direction of fluid flow are as indicated by arrows .Towards right and upwards is positive .

1) For part A) would you agree that "Horizontal Force exerted by tube on liquid " will be $- \rho A v^2 - PA$ , where P is the pressure in the fluid at entry ?

2) For part A) would you agree that "Vertical Force exerted by tube on liquid " will be $- \rho A v^2 - PA$ , where P is the pressure in the fluid at exit ?

3) For part B) would you agree that "Horizontal Force exerted by tube on liquid " will be $- 2 \rho A v^2 - 2PA$ , where P is the pressure in the fluid at entry/exit ?

 

[Chestermiller]

I think I can help with this. We are doing a momentum balance on the fluid in the control volume between the exit of the tank and the exit of the tube. First, the vertical direction. You correctly determined the force that the pipe exerts on the fluid in the vertical direction as $-p_aA-2\rho v^2A$ (aside from the weight of the fluid, which should also have been included).

If the pipe were empty, except for air, and we put an imaginary surface across the exit cross section, and we did a vertical force balance on the pipe (with this exit cross section included), we would have found that the net air pressure force exerted over the entire surface of the pipe would have been zero (for equilibrium to prevail). In this case, the vertical force over the exit cross section would have been $p_aA$ upward, so the vertical air pressure force over the remaining part of the pipe surface (aside from the exit cross section) would have had to have been $p_aA$ downward. But the vertical air pressure force acting over the remaining part of the pipe does not change when fluid is flowing. So, if we include this in the vertical force balance on the pipe when fluid is flowing (together with the force from the fluid), the net downward force of the air $p_aA$ is just canceled out by the upward pressure force from the fluid $p_aA$. So the net resultant vertical force on the pipe when the fluid is flowing is just $2\rho v^2A$.

Of course, as TSny has correctly pointed out, the weight of the fluid in the pipe should also have been included in the vertical force balance on the fluid within the control volume.

As far as the horizontal analysis is concerned, I will only note that the fluid pressure at the entrance cross section of the pipe is $p_a+(2\rho)g\frac{H}{4}$. Virtually all the pressure changes leading up to the entrance cross section (exit cross section of the tank) occur within the tank.

 

[TSny]

In figure A) fluid moves through a pipe which is 3/4th part of a circle whereas in B) the fluid moves through a U tube .The tubes are at rest on a horizontal table which means there must be some support to keep them at place .The direction of fluid flow are as indicated by arrows .Towards right and upwards is positive .

1) For part A) would you agree that "Horizontal Force exerted by tube on liquid " will be $- \rho A v^2 - PA$ , where P is the pressure in the fluid at entry ?

2) For part A) would you agree that "Vertical Force exerted by tube on liquid " will be $- \rho A v^2 - PA$ , where P is the pressure in the fluid at exit ?

3) For part B) would you agree that "Horizontal Force exerted by tube on liquid " will be $- 2 \rho A v^2 - 2PA$ , where P is the pressure in the fluid at entry/exit ?

Yes, I agree with all of these. Again, though, I believe that if you also add in "unbalanced atmospheric pressure" on the tubes you find that all the PA terms go away.