Moment of inertia of a uniform square plate

[lorenz0]

Homework Statement

Find the moment of inertia of a uniform square plate of mass M and side L rotating around an axis through its diagonal.

Relevant Equations

$I=\int r^2 dm$

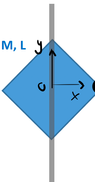
I placed my Oxy coordinate system at the center of the square, the $x$-axis pointing rightwards and the $y$-axis pointing upwards.
I divided the square into thin vertical strips, each of height $h=2(\frac{L}{\sqrt{2}}-x)$, base $dx$ and mass $dm=\sigma h dx=\frac{M}{L^2}2(\frac{L}{\sqrt{2}}-x)dx$, so $I=2\int_{x=0}^{x=\frac{L}{\sqrt{2}}}x^2 \frac{M}{L^2}2(\frac{L}{\sqrt{2}}-x)dx=\frac{5}{12}ML^2$.

However, the solution, according to the exercise, should be $\frac{1}{12}ML^2$ but I haven't been able to see what I am doing wrong so I would appreciate if someone would help me see where my mistake is. Thanks.

 

[Orodruin]

Please show your work in computing the integral.

 

[lorenz0]

Please show your work in computing the integral.

Well... doing the integral for the $n$-th time now I get the correct answer. I don't know why I kept getting it wrong before ...
Here it is:

$I=2\int_{x=0}^{x=\frac{L}{\sqrt{2}}}x^2 \frac{M}{L^2}2(\frac{L}{\sqrt{2}}-x)dx=\frac{4M}{L^2}\int_{0}^{L/\sqrt{2}}(\frac{L}{\sqrt{2}}x^2-x^3)dx=\frac{4M}{L^2}\left(\frac{L}{\sqrt{2}}\int_{0}^{\frac{L}{\sqrt{2}}}x^2dx-\int_{0}^{\frac{L}{\sqrt{2}}}x^3dx\right)=\frac{4M}{L^2}\left( \frac{L}{3\sqrt{2}}\cdot\frac{L^3}{2^{3/2}}-\frac{1}{4}\cdot\frac{L^4}{4} \right)=\frac{4M}{L^2}\left( \frac{L^4}{3\cdot 4}-\frac{1}{4}\cdot\frac{L^4}{4} \right)=\frac{4M}{L^2}\cdot\frac{L^4}{4}\left(\frac{1}{3}-\frac{1}{4}\right)=\frac{1}{12}ML^2.$

 

[Orodruin]

Well... doing the integral for the $n$-th time now I get the correct answer. I don't know why I kept getting it wrong before ...
Here it is:

$I=2\int_{x=0}^{x=\frac{L}{\sqrt{2}}}x^2 \frac{M}{L^2}2(\frac{L}{\sqrt{2}}-x)dx=\frac{4M}{L^2}\int_{0}^{L/\sqrt{2}}(\frac{L}{\sqrt{2}}x^2-x^3)dx=\frac{4M}{L^2}\left(\frac{L}{\sqrt{2}}\int_{0}^{\frac{L}{\sqrt{2}}}x^2dx-\int_{0}^{\frac{L}{\sqrt{2}}}x^3dx\right)=\frac{4M}{L^2}\left( \frac{L}{3\sqrt{2}}\cdot\frac{L^3}{2^{3/2}}-\frac{1}{4}\cdot\frac{L^4}{4} \right)=\frac{4M}{L^2}\left( \frac{L^4}{3\cdot 4}-\frac{1}{4}\cdot\frac{L^4}{4} \right)=\frac{4M}{L^2}\cdot\frac{L^4}{4}\left(\frac{1}{3}-\frac{1}{4}\right)=\frac{1}{12}ML^2.$

It happens. Sometimes you just need a bit of a nudge.

The easiest way to do the integral is to use the substitution $x = Ls/\sqrt 2$, the integral then becomes
$$
I = ML^2 \int_0^1(s^2-s^3)ds = ML^2 \left(\frac 13 - \frac 14\right) = \frac{ML^2}{12}.
$$

An even easier way of doing the problem is noting that, due to the symmetry of the square, the moment of inertia must be the same for any axis lying in the plane of the square and passing through the square center. You can therefore just as well compute the MoI relative to an axis through the center parallel to two sides (and orthogonal to the others). This will be the same as the MoI of a rod relative to its center, i.e.,
$$
I = 2\frac{M}{L}\int_0^{L/2} x^2 dx = \frac{2M}{L} \frac{(L/2)^3}3 = \frac{ML^2}{12}.
$$
Of course, the result is the same - as it should be.