- #1
etf
- 179
- 2
Hi!
Here is my task:
For differential amplifier on scheme calculate voltage gains Av1=vout1/(vin1-vin2) and Av2=vout2/(vin1-vin2). MOSFET's M1 and M2 have same characteristics. MOFSTE's M3 and M4 have same characteristics. All MOSFET's are in saturation. Assume that gm*rds>>1.
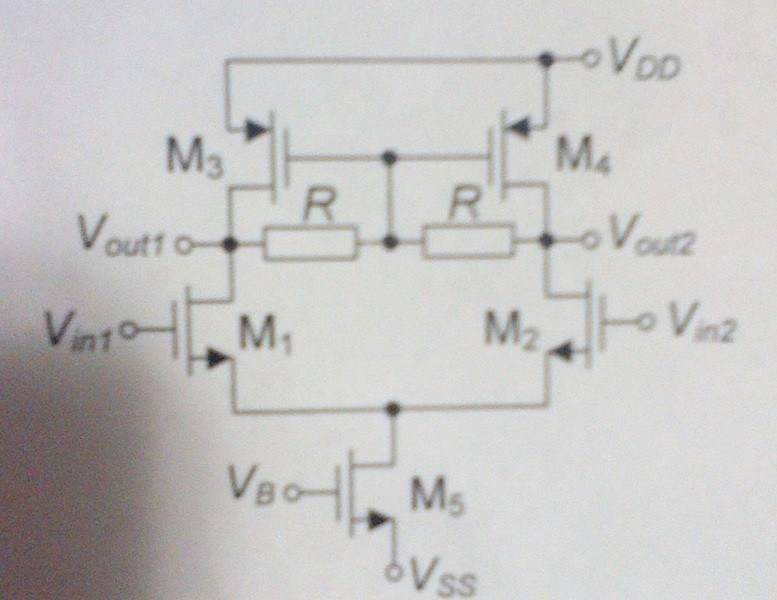
How to use fact that gm*rds>>1?
I did AC Analysis of this amplifier and found vout1 in function of vin1 and vin2 and vout2 in function of vin1 and vin2. For the sake of simplicity, I used variables a,b,... . I got these results:
[itex]vout1=\frac{bgn-cfn+dfm-dgl}{afm-agl-bem+bgk+cel-cfk}\, \, \,\, vin1+\frac{chl-bhm+bgo-cfo}{afm-agl-bem+bgk+cel-cfk}\, \, \, \, vin2 [/itex]
[itex]vout2=\frac{cen-agn-dem+dgk}{afm-agl-bem+bgk+cel-cfk}\, \, \, \, vin1+\frac{ahm-chk-ago+ceo}{afm-agl-bem+bgk+cel-cfk}\, \, \, \, vin2[/itex]
My question is, how to get rid of vin1 and vin2 in Av1 and Av2? V1 and v2 shouldn't figure in gains Av1 and Av2.
Here is my task:
For differential amplifier on scheme calculate voltage gains Av1=vout1/(vin1-vin2) and Av2=vout2/(vin1-vin2). MOSFET's M1 and M2 have same characteristics. MOFSTE's M3 and M4 have same characteristics. All MOSFET's are in saturation. Assume that gm*rds>>1.
How to use fact that gm*rds>>1?
I did AC Analysis of this amplifier and found vout1 in function of vin1 and vin2 and vout2 in function of vin1 and vin2. For the sake of simplicity, I used variables a,b,... . I got these results:
[itex]vout1=\frac{bgn-cfn+dfm-dgl}{afm-agl-bem+bgk+cel-cfk}\, \, \,\, vin1+\frac{chl-bhm+bgo-cfo}{afm-agl-bem+bgk+cel-cfk}\, \, \, \, vin2 [/itex]
[itex]vout2=\frac{cen-agn-dem+dgk}{afm-agl-bem+bgk+cel-cfk}\, \, \, \, vin1+\frac{ahm-chk-ago+ceo}{afm-agl-bem+bgk+cel-cfk}\, \, \, \, vin2[/itex]
My question is, how to get rid of vin1 and vin2 in Av1 and Av2? V1 and v2 shouldn't figure in gains Av1 and Av2.
Last edited:
