Motional EMF problem

[SpectraPhy09]

Homework Statement:

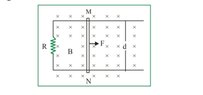
Two long Horizontal rails, a distance d apart and each having a resistanc λ per unit length are joined one end by a resistance R. A perfectly conducting rod MN of mass m is free to slide along the rails without friction v(I have attached the file for the diagram plz check) . There is a uniform magnetic field of induction B Normal to the plane of the paper and directed into the paper. Variable Force F is applied to the rod MN such that, as the rod moves, a constant current i and flows through R.
(i) Find the applied force F as function of distance x of the rod from R.

Relevant Equations:

Force due to a current carrying wire = iBl
Where i = current
B = Magnetic field
L = length of the wire
E.M.F induced due to a rod of length l moving with Velocity V in Magnetic field B = VBl
Its applicable only when V, B and I are mutually perpendicular to each other

I request please go through my solution

Total Resistance = R + 2λx
V(ind) = vBd
I(ind)= vBd/(R + 2λx )
v = i(R + 2λx )/Bd

If force on the wire due to induced current is iBl then
Fnet = iBd - F ...(i)
or Fnet = F - iBd ...(ii)
Fnet = v(dv/dx)
v(dv/dx) = iBd - F

By solving we get
Fnet by (i) is iBd - 2λi²m(R+2λx)/B²d²
(ii)is 2λi²m(R+2λx)/B²d² - iBd

Which one of this is correct ? Or both are correct ? Did I made any mistake in the solution

 

[BvU]

Hello @SpectraPhy09,

$\qquad$ !​

I have attached the file for the diagram please check

I checked -- didn't see a thing !

What I see is two answers, one the opposite of the other ?

$\$

 

[TSny]

If force on the wire due to induced current is iBl then
Fnet = iBd - F ...(i)
or Fnet = F - iBd ...(ii)

I don't see the file for the diagram that you said you attached. It's not clear in which direction the rod is being pushed.

Fnet = v(dv/dx)
v(dv/dx) = iBd - F

Should the mass of the rod appear somewhere in the equations above?

By solving we get
Fnet by (i) is iBd - 2λi²m(R+2λx)/B²d²
(ii)is 2λi²m(R+2λx)/B²d² - iBd

Do these expressions represent F_net or the applied force F?

 

[SpectraPhy09]

I'm really sorry there's a mistake in my soln
Ya m should appear, i.e Fnet = mv(dv/dx)
mv(dv/dx) = iBd - F
The force Is not Fnet it is the applied Varying force F
i.e. F = iBd - 2λi²m(R+2λx)/B²d². ...(i)
Or. F = 2λi²m(R+2λx)/B²d² - iBd ...(ii)

My doubt was which of the equation among (i) or (ii) is correct ?
Or both are correct ?


I have attached the figure please check

 

[Steve4Physics]

mv(dv/dx) = iBd - F
The force Is not Fnet it is the applied Varying force F
i.e. F = iBd - 2λi²m(R+2λx)/B²d². ...(i)
Or. F = 2λi²m(R+2λx)/B²d² - iBd ...(ii)

My doubt was which of the equation among (i) or (ii) is correct ?
Or both are correct ?

Hi @SpectraPhy09. Both equations can't be correct. For example -5 is not equal to +5. In fact neither equation is correct! See if this helps.

We are taking +x as being ’to the right’. And from the question we deduce the rod moves to the right.

In 1-dimension, vectors in the positive direction are represented positive values and vectors in the negative direction by negative values

The applied force, F, acts to the right (given in diagram) so it is represented by a positive value.

As the rod moves right, its (positive) velocity must increase to keep the current constant. (Why?) So the direction of acceleration is to the right. Therefore the direction of the net force is to the right. So the net force is represented by a positive value.

The ‘back-force’ has magnitude = iBd and acts to the left (from Lenz’s law). So we assign it the value -iBd.

We are adding two forces by vector addition:

$\overrightarrow {net force} = \overrightarrow {applied force} + \overrightarrow {back force}$

which in 1-dimension gives
$F_{net} = F + (-iBd)$

Does that make sense?

Neither of your answers:
F = iBd - 2λi²m(R+2λx)/B²d². ...(i)
F = 2λi²m(R+2λx)/B²d² - iBd ...(ii)
are correct. But you are very close!

 

[SpectraPhy09]

@Steve4Physics
Oh is there a +ve instead of -ve ..?
F = iBd + 2λi²m(R+2λx)/B²d²

 

[Steve4Physics]

@Steve4Physics
Oh is there a +ve instead of -ve ..?
F = iBd + 2λi²m(R+2λx)/B²d²

Yes, that's what I get too. Well done!