- #1
jamesbiomed
- 76
- 0
Homework Statement
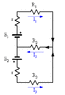
Assuming each battery has internal resistance r = 1.0 Ω, determine the magnitudes and directions of the currents through each resistor shown in the following figure. The batteries have emfs of 1 = 9.0 V and 2 = 12.0 V and the resistors have values of R1 = 15 Ω, R2 = 20 Ω, and R3 = 30 Ω.
Find Current through R1, R2, R3
PLEASE SEE PICTURE:
http://www.webassign.net/gianpse3/26-40.gif
Homework Equations
V=Emf-r*I
V=I*R
The Attempt at a Solution
When two batteries are in a series, their total voltage is the algebraic sum of of their respective voltages.
For R1: I used V=emf-r*I and set it equal to I*R. My first attempt I added the emf's and plugged into the equation and it didn't work. Then I tried adding (emf-r*I)+(emf-r*I) for both eq'ns and setting equal to I*R and was incorrect.
I tried this for all three to no avail.
Since the resistance is given for each, and I'm not adding them, the fact that they are parallel or in a series with each other was not taken into consideration. But I have been getting the feeling that maybe this should have been...
Any help would be really nice