Hercuflea
- 593
- 49
Not sure whether this is an intro physics or intro calculus/related rates problem.
1. Homework Statement
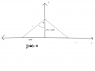
Suppose a point P lies at (x,y)=(0,1) meters.
A car is traveling at 30 meters/second along the x-axis towards +∞.
Define r to be the distance between P and the car at any time t.
I need to know the rate of change of the distance between P and the car with respect to time (dr/dt) ?
Pythagorean theorem...I attached a picture
Attached my attempted solution...tried 2 methods. I do not know what θ(t) or dθ/dt is so that's why I haven't been able to get it.
Attached[/B]
1. Homework Statement
Suppose a point P lies at (x,y)=(0,1) meters.
A car is traveling at 30 meters/second along the x-axis towards +∞.
Define r to be the distance between P and the car at any time t.
I need to know the rate of change of the distance between P and the car with respect to time (dr/dt) ?
Homework Equations
Pythagorean theorem...I attached a picture
Attached my attempted solution...tried 2 methods. I do not know what θ(t) or dθ/dt is so that's why I haven't been able to get it.
The Attempt at a Solution
Attached[/B]