FallenApple
- 564
- 61
I'm watching a vid on the n queens problem. Basically I have find out how to put n queens on a chess board of size n without them attacking each other. It's a rather famous puzzle.
"The eight queens puzzle is the problem of placing eight chess queens on an 8×8 chessboard so that no two queens threaten each other. Thus, a solution requires that no two queens share the same row, column, or diagonal. The eight queens puzzle is an example of the more general n queens problem of placing n non-attacking queens on an n×n chessboard, for which solutions exist for all natural numbers n with the exception of n=2 and n=3."
https://en.wikipedia.org/wiki/Eight_queens_puzzle

here there is no positions after the second level of the recursion. So it makes sense that after the third level of the recursion is popped from the stack, the second level will just continue the for loop.But why is the previous placement replaced?
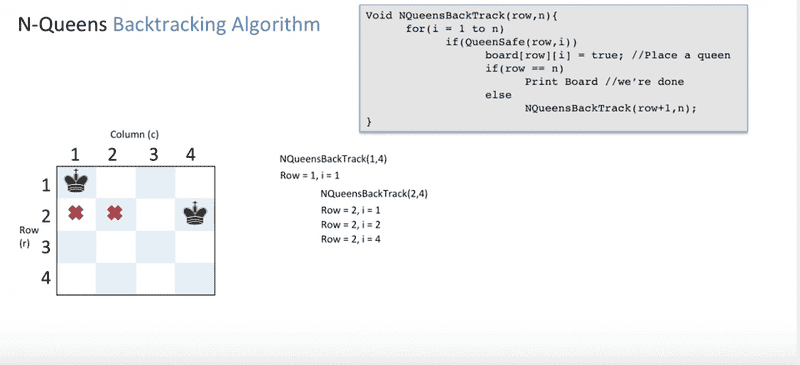
He mentions that when the backtrack happens, the queen is placed on the 4th column. But that is only possible if the previous placement is nullifed. But how? I see nothing in the code that can erase the result of board[2][3]==2.
"The eight queens puzzle is the problem of placing eight chess queens on an 8×8 chessboard so that no two queens threaten each other. Thus, a solution requires that no two queens share the same row, column, or diagonal. The eight queens puzzle is an example of the more general n queens problem of placing n non-attacking queens on an n×n chessboard, for which solutions exist for all natural numbers n with the exception of n=2 and n=3."
https://en.wikipedia.org/wiki/Eight_queens_puzzle
here there is no positions after the second level of the recursion. So it makes sense that after the third level of the recursion is popped from the stack, the second level will just continue the for loop.But why is the previous placement replaced?
He mentions that when the backtrack happens, the queen is placed on the 4th column. But that is only possible if the previous placement is nullifed. But how? I see nothing in the code that can erase the result of board[2][3]==2.