NAP Yr 9 Example Test: Numeracy Q28 - 47.5 cm?

  • Context: MHB 
  • Thread starter Thread starter vincentlu
  • Start date Start date
  • Tags Tags
    Example Test
Click For Summary
SUMMARY

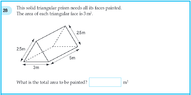
The discussion centers on Question 28 of the NAP Year 9 Example Test, which presents a calculation discrepancy regarding the total area of a geometric figure. Participants confirm that the correct total area is 46 square meters, derived from the formula: 3 + 3 + (5 x 2.5) + (5 x 2.5) + (5 x 3). The confusion arises from misinterpreting units, as one participant mistakenly calculated 47.5 centimeters instead of the correct 46 square meters. The importance of unit conversion is emphasized, as it significantly impacts the final result.

PREREQUISITES
  • Understanding of geometric area calculations
  • Familiarity with unit conversions (meters to centimeters)
  • Basic algebraic manipulation skills
  • Knowledge of triangular and rectangular face areas in geometry
NEXT STEPS
  • Review geometric area calculation methods for various shapes
  • Study unit conversion techniques, particularly between metric units
  • Practice solving similar NAP test questions for improved accuracy
  • Explore common pitfalls in geometry calculations and how to avoid them
USEFUL FOR

Students preparing for the NAP Year 9 Numeracy Test, educators teaching geometry, and anyone looking to improve their mathematical problem-solving skills.

Mathematics news on Phys.org
I get 46 cm². Can you post your work so we can see what you did wrong?
 
View attachment 4369

I get 46 too, but in meters and not in centimeters! (which makes a huge difference) (Sweating)

Areas of triangular faces are already given. We just need to find separate areas of all rectangular faces and add all triangular-face-areas to rectangular-face-areas in order to get the total area.

$$3+3+(5 \times 2.5)+(5 \times 2.5)+(5 \times 3) = 46 \text{m}^{2}$$

Also, I tried many experiments to find a situation where someone gets confused and gets the answer as $$47.5$$ by mistake, but found no such situation!
 

Attachments

  • picture.png
    picture.png
    8.6 KB · Views: 79

Similar threads

High School Chi-Square Tests for Homogeneity & Association
  • · Replies 7 ·
Replies
7
Views
2K
MHB Calculating Probabilities in Poker Hand: An Example
  • · Replies 1 ·
Replies
1
Views
2K
MHB Dylan's questions at Yahoo Answers regarding related rates
  • · Replies 4 ·
Replies
4
Views
5K
Radius of a planet with the same density as Neptune
  • · Replies 13 ·
Replies
13
Views
4K
MHB How Do I Correctly Apply the Alternating Series Test?
  • · Replies 1 ·
Replies
1
Views
2K
Graduate Do You Have What it Takes to Be a True Mathematician?
  • · Replies 21 ·
Replies
21
Views
4K
Undergrad Examples of units with non-integer exponents
  • · Replies 2 ·
Replies
2
Views
3K
What Is the Net Thermal Radiation Transfer Rate for a Stretched Cylinder?
  • · Replies 3 ·
Replies
3
Views
7K
Electronics Quiz Concerned with how accurately things were marked
  • · Replies 10 ·
Replies
10
Views
3K
What is the current in this circuit?
  • · Replies 3 ·
Replies
3
Views
2K