Need help finding the restraining reaction force for a beam

[Kile]

1. The illustrated structure is affected by a known couple, and try to figure out the restraining reaction force of the hinge A and hinge E.

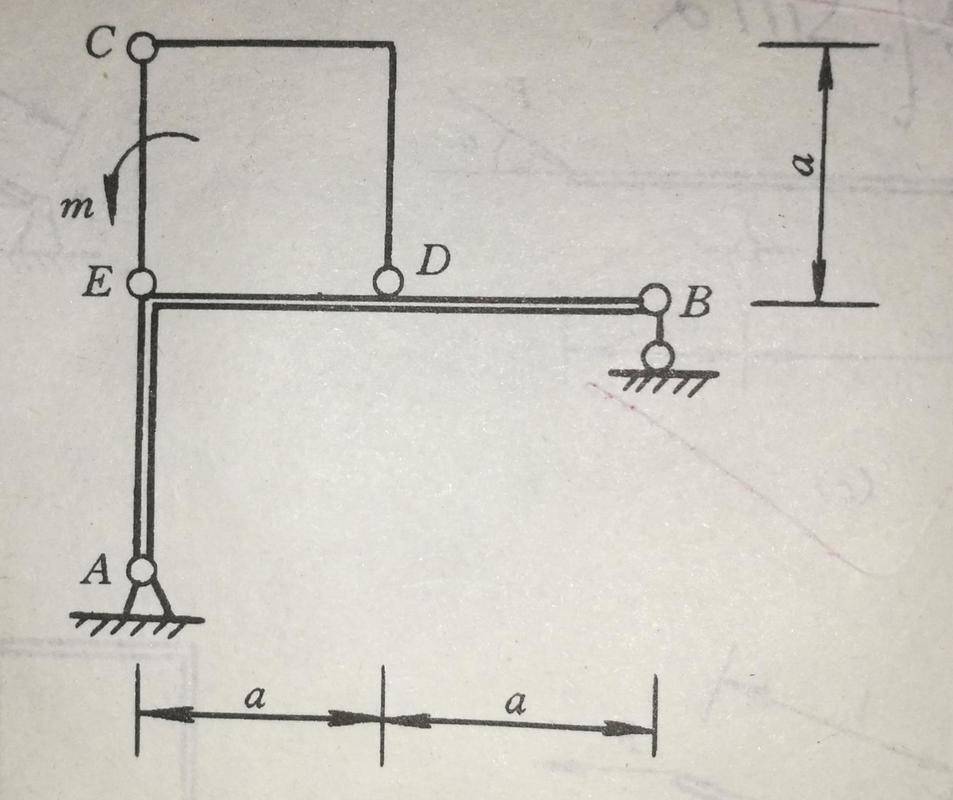
We should analyse ECD instead. Since arm CD is a two force members, so N(C) in in the direction where CD connects by these two points. The distance from E to diagonal CD is a/√2. So we have N(C)=√2 m/a. Because N(C)=N(E) ( N(C) and N(E) together form a couple), N(E)=√2 m/a.
Where did I go wrong?

 

[haruspex]

Where did I go wrong?

I agree with your reasoning and answer. Who says it is wrong? What other answer is given ?

 

[Kile]

I agree with your reasoning and answer. Who says it is wrong? What other answer is given ?

The official answer just doesn't match mine.

 

[haruspex]

The official answer just doesn't match mine.

Ok, but what is the official answer?

 

[Kile]

R_A= \frac m 2a, R_E=\frac \sqrt {{2} m} a,

 

[haruspex]

Your latex had some errors. In fixing it up I arrived at

$R_A= \frac m{ 2a}$, $R_E=\frac {\sqrt {2} m} a$,

But that makes the reaction at E the same as you got, so perhaps you meant something else.

 

[Kile]

Your latex had some errors. In fixing it up I arrived at

But that makes the reaction at E the same as you got, so perhaps you meant something else.

Yes. You did it in the right format. Do u know how to get this official answer?

 

[haruspex]

Yes. You did it in the right format. Do u know how to get this official answer?

As I wrote, it's the same as your answer, just written differently. They both say $(\sqrt 2)(\frac ma)$.

 

[Kile]

How did u get $N_A$ ?
Can u draw a diagram to illustrate?

 

[haruspex]

How did u get $N_A$ ?
Can u draw a diagram to illustrate?

I thought we were discussing N_E.
For N_A, take moments about the other hinge.

 

[Kile]

How can u get it? can u help me out?

 

[haruspex]

How can u get it? can u help me out?

Consider the whole frame as one body. If you take the B hinge as axis, what moments are there?

 

[Kile]

Because point B has a pulley on the ground, $N_B$ is vertical.
Choose A be centroid
$$\sum m_A (F)=0, ~2a N_B + m=0$$
$$\Rightarrow N_B=\frac {-m} {2a},$$ So it's downward.
X-axis, $$X_A=0$$
Y-axis, $$Y_A=0 $$ $$N_B + Y_A=0$$
$$\Rightarrow Y_A= -N_B = \frac {m} {2a}$$ So $Y_A$ it's upward.

 

[haruspex]

View attachment 240415 Because point B has a pulley on the ground, $N_B$ is vertical.
Choose A be centroid
$$\sum m_A (F)=0, 2a N_B + m=0$$
$$\Rightarrow N_B=\frac {-m} {2a},$$ So it's downward.
X-axis, $$X_A=0$$
Y-axis, $$Y_A=0 $$ $$N_B + Y_A=0$$
$$\Rightarrow Y_A= -N_B = \frac {m} {2a}$$ So $Y_A$ it's upward.

Right... except, strictly speaking there could be equal and opposite horizontal forces at A and B, making the problem indeterminate.

 

[Kile]

Right... except, strictly speaking there could be equal and opposite horizontal forces at A and B, making the problem indeterminate.

You mean $$X_A = X_ B$$ It may not equals to 0.
We just can't calculate it from the information already given.
Is that what you are trying to say here?

 

[haruspex]

You mean $$X_A = X_ B$$ It may not equals to 0.
We just can't calculate it from the information already given.
Is that what you are trying to say here?

Right, except X_A=-X_B. And if not zero then it changes Y_A and Y_B so as to balance the torque.