Need help in creating a question that uses the word asymptote

[Bridgette]

Hello everyone.

Currently I teach a test prep course that covers a multitude of subjects. One specific area of the test covers Math Algebra, Trigonometry etc.

My employee is a Math teacher who doesn't understand that sometimes the students (all of whom are adults) cannot get past the LANGUAGE in the question at times and panic and give up before they even attempt to answer the question.

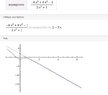
Since the test we prep for doesn't cover calculus or pre-calculus, when they see a question with the word asymptote in the question, they do not understand that they are not being asked to solve for asymptote. If we introduce the word to them, it's so far beyond what they need to know that they shut down or get very very confused.

I would like some help in creating an accurate math question that uses the word asymptote only to identify the line approaching the curve. The actual question is asking them for the SLOPE of the line.

I have asked my Math teacher for an example of this for over a week now and I'm at my wits end because since he's a math expert, he doesn't understand how much they panic and give up on the test.

Help

 

[Joppy]

Welcome to the forum!

Since the test we prep for doesn't cover calculus or pre-calculus, when they see a question with the word asymptote in the question, they do not understand that they are not being asked to solve for asymptote. If we introduce the word to them, it's so far beyond what they need to know that they shut down or get very very confused.

I would like some help in creating an accurate math question that uses the word asymptote only to identify the line approaching the curve. The actual question is asking them for the SLOPE of the line.

I have asked my Math teacher for an example of this for over a week now and I'm at my wits end because since he's a math expert, he doesn't understand how much they panic and give up on the test.

I'm afraid i don't understand how this is ever going to work.

Either the students need to understand the meaning and context of asymptote's, or you don't test them on it.

So, is working with asymptotic curves part of the curriculum? If they are indeed required to understand what it means, and be able to work with it in the context of a problem, then the only reasonable solution would be to try your best to help them understand.

The actual question is asking them for the SLOPE of the line.

Are we talking about one specific question that is going to be on their test?

EDIT: Sorry if my response seems blunt. I just hate the thought of giving the students an option to give into fear of math as an alternative to working through the math.

 

[Bridgette]

No I appreciate the bluntness of it. It's a really tricky test to prep for because they will randomly throw in questions. One of the big problems I have in getting support for the classes is that when we hire the Math teachers they always want them to understand the real Math intellectually. If these were Math people or this in any way related to them really understanding Math, I would agree with them. But this isn't.

It would be something similar to taking a Nursing Home worker and not allowing them to work in the nursing home, even though they passed all their credentialing in medicine, until they passed this one last test in random Math questions.

For many of these test takers, they haven't taken math in years and totally give up halfway through the question if they see a word they don't know.

We run a one day booster workshop so I don't have time to go over everything they don't know. We also have a mix of Math abilities so I have had classes where people know a lot of Math and then other people who don't even understand a Multiplicative Inverse in the same class. Keep this in mind. Most Math classes have students grouped by ability.So far we've had great success in getting them to not only pass the test, but also change how they feel about Math. More and more of them are actually understanding it.

I just need help in creating a few sample questions for their homework packet.
It's not as if the test says we're testing for Algebra. It's a smattering of all different levels of Math from Operations, all the way up to Trigonometry. But since there are only 40 questions there may be one question about slope, one question about perimeter of a cube.

What I have tried to do is find a common thread in questions that we can teach them. For example many different questions can be solved using Pythagorean Theorem. I really want to reassure you that we are not trying to show them how to "cheat" or "do math the wrong way" it's just that most people panic and don't even try to understand the question.

If you want to understand what I deal with, look up on Youtube -- Patricia Heaton Math. This is what I'm trying to address. I do NOT want them to give into the fear.

I'm trying to get them to see that if you don't panic, you can actually answer the question.For example, I found this question on asymptote on another post. You don't actually even need to know what asymptote means to answer the question. You just use long division. I'm trying to get the them to understand that you can do the math in the question even if you don't quite grasp what asymptote means.View attachment 6442