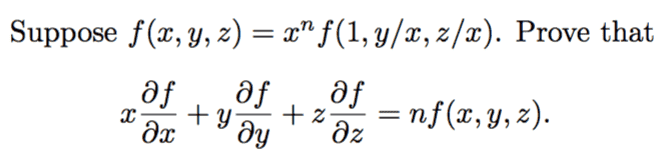SUMMARY
The discussion focuses on applying the chain rule in multivariable calculus, specifically in the context of the function defined as ##f(x,y,z)=x^nf(1,y/x,z/x)##. Participants clarify that to prove ##f(tx,ty,tz)=t^nf(x,y,z)##, one must correctly substitute variables into the initial equation. The key takeaway is that by applying the chain rule correctly, users can derive the necessary relationships to complete the proof.
PREREQUISITES
- Understanding of multivariable calculus concepts
- Familiarity with the chain rule in calculus
- Ability to manipulate and substitute variables in mathematical functions
- Knowledge of function notation and properties
NEXT STEPS
- Study the application of the chain rule in multivariable functions
- Explore proofs involving homogeneous functions
- Learn about substitution techniques in calculus
- Review examples of function transformations in multivariable calculus
USEFUL FOR
Students and educators in mathematics, particularly those studying calculus, as well as anyone looking to deepen their understanding of multivariable function proofs and the chain rule application.