Need help with my Swinging Ball problem please

[SnowboardNerd]

Homework Statement

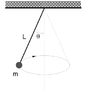
A mass m = 16.0 kg is attached to the lower end of a massless string of length L = 63.0 cm. The upper end of the string is held fixed. Suppose that the mass moves in a circle at constant speed, and that the string makes an angle theta = 17o with the vertical, as shown in the figure. How long does it take the mass to make one complete revolution?

Homework Equations

T = 2 pi r / v

F = m a

Ac = v^2 / r

The Attempt at a Solution

m = 16
L = 0.62 m
θ = 17

Drew a FBD...
It shows mg acting down upon the object, and T diagonally up.


Fx = m * ac
T sin theta = m ac
T sin theta = m * v^2/r
T sin theta = m * v^2/ L sin theta

Fy = m * ac
T cos theta - mg = 0
T cos theta = mg
T = mg /cos theta

Use the above and sub it in..

(mg/cos theta) sin theta = m (v^2) / L sin theta

√ ((( L (sin(theta))^2) g sin(theta))) / cos theta ) = V

V = (sqrt( (.63 (sin^2(17)) (9.8) sin(17) )/ cos(17)))

Use formula... T = 2pi r / v

(2pi(0.63*sin(17)))/(sqrt( (.63 (sin^2(17)) (9.8) sin(17) )/ cos(17)))

I get.. 2.88 seconds.

Where did I go wrong?? Thanks for your time!

 

[SnowboardNerd]

Is there anything else I need to include to get help?

 

[SammyS]

Patience.

Draw a Free Body Diagram for the ball. (never mind.)

 

[SnowboardNerd]

**** you all, this website is ********. you guys never actually respond and when you do its useless. suck a cows dick. I'm out.

 

[SnowboardNerd]

I did it perfectly... all I did wrong was that I unnecessarily squared an sin theta and you faggots couldn't tell me that. this site is useless...

 

[SammyS]

I get that \displaystyle v^2=\frac{gL\,\sin^2(\theta)}{\cos(\theta)}\,.

It's hard to say what you have for v. There is a severe case of unbalanced parentheses.

 

[SammyS]

**** you all, this website is ********. you guys never actually respond and when you do its useless. suck a cows dick. I'm out.

I did it perfectly... all I did wrong was that I unnecessarily squared an sin theta and you faggots couldn't tell me that. this site is useless...

That's probably NOT the way to get help.