Need help with parallelogram proof

In summary, the conversation discusses the use of congruent angles and sides in a parallelogram to establish similarity between triangles. The speaker is struggling to understand how this proves a specific proportion involving sides of the triangles. They are advised to focus on the similarity of triangles SXY and SVT and use the fact that opposite sides of a parallelogram are equal to solve the problem.
  • #1
sc00t34
1
0
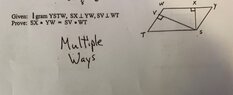
Hello, we are learning about similar triangles and this was a problem. So I know that opposite sides of a parallelogram are congruent as are opposite angles, so I can establish similarity with triangles WYS and STW, but I don't understand how that proves SX x YW = SV x WT because the proportions don't match up when I compare similar triangles for their corresponding parts.

Any help is greatly appreciated... am I on the right track?

This is what I have so far. See attached image.

Statement Reason

1. WYST is Parallelogram. 1. Given
2. angle Y and angle T are congruent. 2. Def of parallelogram, opposite angles congruent.
3. WT and YS congruent, WY and TS congruent. 3. Def of parallelogram, opposite sides congruent.
4. WYS and STW are similar. 4. SAS
?
 

Attachments

  • IMG_0700 copy.jpg
    IMG_0700 copy.jpg
    12.7 KB · Views: 91
Mathematics news on Phys.org
  • #2
The similar triangles that you need to look at are $SXY$ and $SVT$. Then use the fact that opposite sides of the parallelogram are equal.
 

FAQ: Need help with parallelogram proof

What is a parallelogram proof?

A parallelogram proof is a mathematical argument or demonstration that uses logical reasoning and geometric principles to prove that a given shape is a parallelogram. It involves identifying and using the properties of parallelograms, such as opposite sides being parallel and congruent, to show that the shape in question meets all the criteria of a parallelogram.

How do I start a parallelogram proof?

The first step in a parallelogram proof is to identify the given information and what you are trying to prove. Then, use the properties of parallelograms to make logical deductions and draw conclusions. You can also use theorems and postulates related to parallelograms, such as the opposite sides and angles theorem, to help guide your proof.

What are the common properties of parallelograms used in proofs?

Some of the most commonly used properties of parallelograms in proofs include opposite sides being parallel and congruent, opposite angles being congruent, consecutive angles being supplementary, and diagonals bisecting each other. These properties can be used to prove that a given shape is a parallelogram or to solve for missing measurements in a parallelogram.

Can I use algebra in a parallelogram proof?

Yes, algebra can be used in a parallelogram proof to solve for missing measurements or to show that two expressions are equal. For example, if you are given the measurements of two sides of a parallelogram and are trying to find the length of a third side, you can use algebra to set up and solve an equation based on the properties of parallelograms.

Are there any tips for writing a clear and concise parallelogram proof?

One tip for writing a clear and concise parallelogram proof is to clearly label all given information and the steps of your proof. This will help you keep track of what you have already proven and what you still need to show. Additionally, it can be helpful to draw diagrams and use colors or symbols to represent different parts of the parallelogram, making it easier to visualize and understand the proof.

Similar threads

MHB Proving the Angle-Angle-Side Theorem
Replies
1
Views
2K
MHB Proof of Parallelogram ABCD: Midpoint X & Y Show Area $\frac{1}{4}$
Replies
5
Views
2K
MHB Prove Equal Area Triangle & Parallelogram, $\angle ADC=90^{\circ}$
Replies
9
Views
3K
MHB What are the angles of isosceles triangle ABC?
Replies
1
Views
957
MHB Find value of x and area of parallelogram: a,b,c,P
Replies
2
Views
2K
Proof of Parallelogram Theorem: 2 Pairs of Opposite Angles Congruent
Replies
2
Views
15K
MHB Proving Perpendicularity of Two Segments
Replies
4
Views
2K
MHB Show that AN=1 cm using the knowledge of equiangular triangles.
Replies
9
Views
2K
MHB Triangle two column proof question
Replies
1
Views
6K
Understanding the Parallelogram Area Formula: A Quest for Proof
Replies
9
Views
4K

Hot Threads

Recent Insights

Back
Top