Newton Raphson method (convergence problem)

In summary, the conversation discusses the issue of non-convergence in a FORTRAN code using the Newton Raphson method. The code is for a program called Free_energy and involves calculations for the convergence of results. One person suggests increasing the number of iterations and checking for convergence. They also mention making changes to the code for better programming style. The conversation ends with a request for advice or direction in this case.
  • #1
KarAnw
3
0
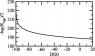
Hello, I am new in the field of FORTRAN. I started to write a code using Newton Raphson method. Below is the code of main program portion only. During my calculation, I have found that my results are not converging, Any help or advice will be highly appreciated in this case.
Thank you for the effort of helping in advance. Program Free_energy
Implicit None
Integer:: i,j,l,k
Double Precision Gmic,U,Phi
Double Precision s,Uderv,cc,DG0,cf,ctot1,
& Keff,Cagg,ctot,sum,Cagg1,cnew,
& Cagg2,cctot1,kapp,error,Csalt,Csalt1,
& cext
Double precision :: Nelec
Double precision :: Nwat
Double precision :: Nlig

ctot = 1D0
cf=ctot/2
cext = 0.01

sum=0.0
DG0 = -100.0

Do While(DG0.le.20)

do i=0,2
do j=0,10
do l=0,10

Nelec=i
Nwat=j
Nlig=l

Keff=dexp(-Gmic(Nelec,Nwat,Nlig)-Nelec*DG0)
Cagg=Keff*((cf)**Nlig)
Cagg1=sum+Nlig*Cagg
Cagg2=sum+(Nlig**2)*Cagg

enddo
enddo
enddo

ctot1=ctot-Cagg1
cctot1=ctot-Cagg2

cnew = cf-(ctot1/cctot1)

error = abs((cnew-cf)/cnew)

cf = cnew

write(72,*) cf, error
if(error.lt.1D-7) exit

Csalt1 = 0.0

do i=0,2
do j=0,10
do l=0,10

Nelec=i
Nwat=j
Nlig=l

Keff = dexp(-Gmic(Nelec,Nwat,Nlig))
Csalt = Csalt1+Keff*((cf)**Nlig)*Nelec

enddo
enddo
enddo

Kapp = Csalt/cext

write(70,*) DG0, -log(kapp)/2
write(72,*) cf, -log(kapp)/2

DG0 = DG0 + 0.1

enddo
 
Technology news on Phys.org
  • #2
I find that graphing the results of the iterations can be helpful.
 
  • #3
Up the number of iterations and check for their convergence...it seems to me at first glance that you are not iterating enough.
 
  • #4
First I would like to thank you both for the reply,

Since you have mentioned that increasing the iteration number may solve the problem, but my question is how can I do that?

Also in my code, the function has summation over an exponential series of the Gimc, I am afraid of that also because I think that summation is also not happening there properly.
Further, I made two changes in the expression of the derivative of my function (Cagg2) and the expression of Keff in my code. The rest of the code is unchangeable and almost like the previous one except that two lines. I ran this one and I find this plot (-log(Kapp)/2 vs DG0) attached with this reply. My aim was to calculate the "cf" which has also the negative values in the calculated results.

I would like to thank you again for the help. Any advice or direction in this case will become helpful to me in near future.

Note: For your interest, the new corrected version of the code (only the main program portion only) has been given below,

Program Free_Energy
Implicit None
Integer:: i,j,l,k
Double Precision Gmic,U,Phi
Double Precision s,Uderv,cc,DG0,cf,ctot1,
& Keff,Cagg,ctot,sum,Cagg1,cnew,
& Cagg2,cctot1,kapp,error,Csalt,Csalt1,
& cext
Double precision :: Nelec,kB,T
Double precision :: Nwat
Double precision :: Nlig

ctot = 1D0
cf=ctot/2
cext = 0.01

DG0 = -100.0
Do While(DG0.le.20)

do i=0,2
do j=0,10
do l=0,10

Nelec=i
Nwat=j
Nlig=l

Keff=dexp(-Gmic(Nelec,Nwat,Nlig)-Nelec*DG0)
Cagg=Keff*((cf)**Nlig)
Cagg1=sum+Nlig*Cagg
Cagg2=sum+(Nlig**2)*Keff*((cf)**(Nlig-1)) enddo
enddo
enddo

ctot1=ctot - Cagg1
cctot1=ctot - Cagg2
cnew = cf-(ctot1/cctot1)

error = abs((cnew-cf)/cnew)

cf = cnew

write(74,*) cf,error

if(error<1D-7)exit

Csalt1 = 0.0

do i=0,2
do j=0,10
do l=0,10

Nelec=i
Nwat=j
Nlig=l

Keff = dexp(-Gmic(Nelec,Nwat,Nlig))
Csalt = Csalt1+Keff*((cf)**Nlig)*Nelec

write(73,*) cf
enddo
enddo
enddo

Kapp = Csalt/cext

write(70,*) DG0, -log(Kapp)/2

write(72,*) cf, -log(Kapp)/2

DG0 = DG0 + 0.1

enddo
End
 

Attachments

  • app_free.png
    app_free.png
    4.5 KB · Views: 514
  • #5
part of your issue is that for example you define Nwat as a double, then assign an integer to it, yes it theoretically works, but better programming style is

Nwat = double(j)

it makes a double out of the j so that it is j.00000000
 
  • #6
Thank you for the reply, I will follow your suggestion and let you know about the result.
 

Related to Newton Raphson method (convergence problem)

1. What is the Newton Raphson method?

The Newton Raphson method is an algorithm used to find the roots of a function. It is a numerical method that uses an initial guess to iteratively improve the approximation of the root.

2. How does the Newton Raphson method work?

The method starts with an initial guess for the root, then uses the derivative of the function at that point to find the slope of the tangent line. The intersection of the tangent line and the x-axis gives a new and improved guess for the root. This process is repeated until the desired level of accuracy is achieved.

3. What is the convergence problem in the Newton Raphson method?

The convergence problem occurs when the method fails to find a root or converges to a wrong root. This can happen due to various factors such as choosing a bad initial guess, encountering a singular point or an inflection point, or the function having multiple roots.

4. How can the convergence problem be addressed?

There are a few ways to address the convergence problem. One approach is to carefully choose a good initial guess that is close to the actual root. Another approach is to modify the algorithm to handle singular or inflection points. Additionally, using a combination of different root-finding methods can increase the chances of finding the correct root.

5. What are some applications of the Newton Raphson method?

The Newton Raphson method is commonly used in various fields such as engineering, physics, and economics to solve equations and find roots of functions. It is also used in optimization problems and in finding critical points of functions.

Hot Threads

Recent Insights

Back
Top