Newton's Law of Gravitation problem

[Shadow Cloud]

In Figure 13-34, a square of edge length 22.0 cm is formed by four spheres of masses m1 = 7.00 g, m2 = 3.50 g, m3 = 1.50 g, and m4 = 7.00 g. In unit-vector notation, what is the net gravitational force from them on a central sphere with mass m5 = 2.30 g?

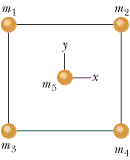
Okay this is what I did so far.
Since m4 and m1 are equal, they can be neglected. This leaves...

F = Gm5(m2-m3) / r^2

I then tried to multiply it by cos 45 degrees to get the i component and sin 45 degrees to get the y component, but this isn't working. Why is that?

 

[emptymaximum]

try defining your own unit vector r in the direction from m3 straight to m5.
then R= rr. Finding r is easy. The force will also be along r, so now the problem is really easy because you won't need trig functions.
If you were explicitly told to use x, y unit vectors then you'll have to change it back.

 

[Shadow Cloud]

What is rr in the equation of R = rr that you gave?

 

[emptymaximum]

R is the vector from m3 to m5. -R would be the vetor from m2 to m5. r is the unit vector in the direction of R.
r is the magnitude of R and is given by √(x²+y²).
r is found the same way, using the magnitudes of the unit vectors.
just be careful where you put the √2 in the unit vectors.
you want to have the r unit vector. remember what it means to be a unit vector.

 

[Shadow Cloud]

I'm kind of following this, but why is the root 2 necessary and where would I put it?

 

[BananaMan]

I'm kind of following this, but why is the root 2 necessary and where would I put it?

a simpler way seen as m1 and m4 cancel may be to work out the 2 forces sepetately using the formula you have already put at the top of the page

seen as they are opposite simply subtract one magnitude from the other (larger - smaller to stop any sign problems) then from that you will have the force and the direction of the line of action of the force, then express this in vector form

sorry if this isn't the way you have been taught but first time i have tried to post a solution on this forum :)

 

[Shadow Cloud]

Oh nevermind, I finally figure out the necessity of the root 2. It's pertains to the length of a diagonal of a square.

 

[emptymaximum]

that's right, it's from the diagonal of the square.

and it's the same thing you'd get if you did trig, but this is, in my opinion, easier and makes more sense.
not only that the ability to perform transformations by means of unit vectors is a very important thing.
/s