PFfan01
- 88
- 2
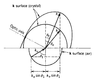
Consider reflection and refraction of a plane light wave on a vacuum-uniaxial crystal interface.
As it is well-known, when the optical axis of the uniaxial crystal is parallel or perpendicular to the normal vector of the interface, there is no double refraction for a natural (unpolarized) light at normal incidence.
For the optical axis neither parallel nor perpendicular to the normal vector, it seems to me, also there is a no-double-refraction case, where the incident angle is set so that the refractive waves (both o-ray and e-ray) propagate along the optical axis. However I failed to find any textbooks which presents such a case. Did I miss something?
As it is well-known, when the optical axis of the uniaxial crystal is parallel or perpendicular to the normal vector of the interface, there is no double refraction for a natural (unpolarized) light at normal incidence.
For the optical axis neither parallel nor perpendicular to the normal vector, it seems to me, also there is a no-double-refraction case, where the incident angle is set so that the refractive waves (both o-ray and e-ray) propagate along the optical axis. However I failed to find any textbooks which presents such a case. Did I miss something?