Non-Constant Angular Acceleration

[DCELL]

TL;DR

Solving for time to rotate 90 degrees with varying angular acceleration

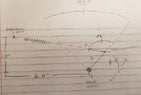
Hello, I am trying to solve a problem involving a mass with known moment of inertia about an axis with a lever arm at angle theta and length r with a non-constant spring force acting at the tip of the lever arm and fixed distance away from the axis of rotation.

I am wondering what the best way to solve for the time to rotate 90 degrees is without assuming the angular acceleration due to torque is constant.

I thought about solving for the acceleration in .1deg intervals using the equation T = alpha * I, and then using that acceleration to calculate the angular velocity at that degree interval using the previous velocity as the "initial" and so on and so forth and finally taking the change in angular velocities between intervals to solve for the time between and then summing the interval times for a total time. I'm not sure if this is the correct approach.

Any help would be appreciated!

Thanks!

 

[Dale]

Are you familiar with calculus?

 

[DCELL]

It's been a semester or two but yes.

 

[Dale]

So then we have $\vec r \times \vec F= I \ddot \theta$. Indeed, depending on the form of $\vec F$ there may not be an analytical solution so you may have to compute it numerically

You also may find a Lagrangian approach to be helpful if $\vec F$ is difficult to figure out.

 

[DCELL]

So I am able to calculate what $\tau$ is and subsequently $\alpha$ for each "iteration" that I have. The point of confusion comes in when I am trying to solve for the Total time of the event. Currently what I've tried is using the equation $\omega_f^2 = \omega_i^2 + 2\alpha\theta$ and treating $\omega_f$ as the current iteration velocity and $\omega_i$ as the initial/previous except for the first iteration where it is equal to zero.

Then using $\omega = \omega_i + \alpha t$ I solve for the time in between the steps where the total time between steps is the time of the event where $\alpha$ was the previous iterations acceleration due to that force/torque.

I've also thought about using $\theta = \omega_i t + \frac 1 2 \alpha t^2$ and solving for t using the quadratic equation which yields similar results as the above

I'm just not confident in the validity of the results and if using the equations for constant acceleration in specific reference frames (every .1deg) is a valid method.

 

[Dale]

If the equation cannot be solved analytically then you will be better served to use something like the basic Stormer Verlet algorithm described here:

https://en.m.wikipedia.org/wiki/Verlet_integration

This uses a fixed step in time rather than a fixed step in space.

 

[DCELL]

If the equation cannot be solved analytically then you will be better served to use something like the basic Stormer Verlet algorithm described here:

https://en.m.wikipedia.org/wiki/Verlet_integration

This uses a fixed step in time rather than a fixed step in space.

Thank you for the information - Ill give this a shot!