Roger44
- 79
- 1
Hi everbody
My plots seem to show that conductivity between two nails immersed a few mm in tap water falls off at low voltages instead of being a horizontal flat line as would be the case for a linear ohmic medium. And the deeper the immersion, the less linear the conductivity. Is this normal or an experimental error?
I measured 50Hz AC current between two stainless steel nails in cold tap water in a small round dish at 5 different voltages, and repeated at five depths (a few mm)
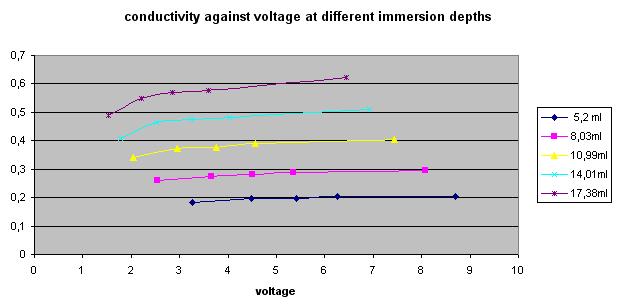
My plots seem to show that conductivity between two nails immersed a few mm in tap water falls off at low voltages instead of being a horizontal flat line as would be the case for a linear ohmic medium. And the deeper the immersion, the less linear the conductivity. Is this normal or an experimental error?
I measured 50Hz AC current between two stainless steel nails in cold tap water in a small round dish at 5 different voltages, and repeated at five depths (a few mm)