How to Find Radial and Tangential Acceleration in Non-Uniform Circular Motion?

[aali069]

Homework Statement

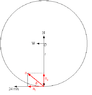
car travels in a flat circle of radius r. at certain point instantaeous velocity is 24 m/s west and the total acceleration is 2.5 m/s2 53 degrees north of west. find radial and tangential acceleration. and period

Homework Equations

ar= 2.5cos37
at=2.5sin37
r=24 x 24/ar
T= 2pie(r)/v

am i plugging in the numbers for ar and at correctly??

 

[aali069]

i got ar to = 1.99 roughly 2 m/s2 and at = 1.5 m/s2
i just am not sure if i use 53 degrees as the angle or 37
using the numbers above i got 288 m for the radius and 74 s as the period..if someone can verify my work and let me know if I am on the right path that would be great..thanks for your help in advanced :)

 

[aali069]

btw here's the actual question if there isn't enough information

a car travels in a flat circle of radius R. at a certain instant the velocity is 24 m/s west, and the total acceleration of the car s 2.5 m/s2 53 degrees north of west. find the radial and tangential components of the acceleration of the car at that moment. if the cars tangential acceleration is constant how long will it take for to make one full cirlce from the point at which its velocity is 24 m/s

 

[gneill]

Use the 53° angle, since it's measured "north of west" and at the instant of interest the car is at the southernmost point of the track and traveling west.

Your period seems a bit high. How exactly did you go about calculating it? Can you show your calculation?