Normalisation constant for identical particles

[WWCY]

In my lecture notes, the normalisation for such a bosonic state was given by

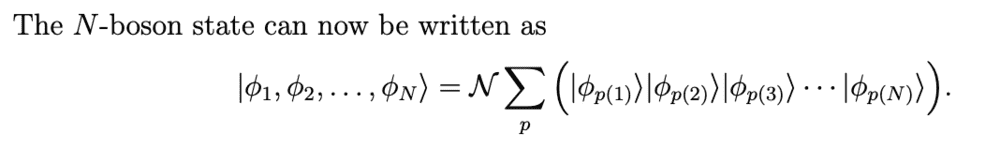
However, I can't quite seem to grasp how the normalisation factor came about. Could someone walk me through it? Many thanks in advance!

 

[vanhees71]

Let's start with clarifying the notation. First of all you have $N$ copies of the one-particle Hilbert space. The space for the $N$-particle system is a subspace of the product space
$$\mathcal{H}_N=\underbrace{\mathcal{H}_1 \otimes \mathcal{H}_1 \otimes \mathcal{H}_1}_{N \quad \text{factors}}.$$
Now the indistinguishability argument comes into the game and then a more complicated topological argument that of all representations of the group of permutations of $N$ particles (the symmetric group $S_N$) only the trivial one (bosons) and the alternating one (fermions) play a role.

Now for bosons you can build a orthonormal basis of the appropriate $N$-particle Hilbert space by using the orthonormal basis $|\phi_a \rangle$ of the one-particle space and build the completely symmetrized products. The corresponding unnormalized basis vectors are
$$|\Psi \rangle=|\phi_1,\ldots \phi_N \rangle^{(+)}=\sum_{P \in S_N} |\phi_{P(1)},\ldots,\phi_{P(N)} \rangle.$$
To normalize it properly, you must also know, how many of the $N$ single-particle states are in the same state, given by $n_a$. The product states are all orthogonal so the normalization factor of the symmetrized state indeed is
$$\langle \Psi|\Psi \rangle=N! \prod_a n_a!$$
which is in the denominator under the square root of your formula.

Let's make this clear on the example of a three-particle state. Say, there are two particles in the state $|\phi_1 \rangle$ and one particle in state $|\phi_2 \rangle$. Then the fully symmetrized state is immediatly given without formally summing over the entire symmetric group of 3 elements as
$$|\Psi \rangle = A (|\phi_1,\phi_1,\phi_2 \rangle + |\phi_1,\phi_2,\phi_1 \rangle + |\phi_2,\phi_1 \phi_1 \rangle,$$
and $A=1/\sqrt{3}$.

If you do the formal sum instead you first write the very same product states more than once coming from the interchanges of the two particles in one and the same state $|\phi_1 \rangle$. The corresponding factor is given by the number of possibilities to order the two equal states, which is $2!$. Then there's always an overall factor $N!$ which is the number of permutations of all $N$ particles.