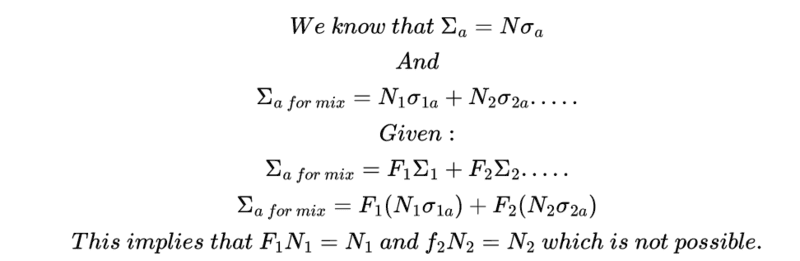SUMMARY
The discussion centers on the calculation of the macroscopic cross-section for a mixture of two species, specifically using the equation $$\Sigma_a^{(mix)} = f_1 \Sigma_{a1}^{(norm)} + f_2 \Sigma_{a2}^{(norm)}$$. Participants clarify the relationship between the number density of constituents in a mixture and their normal densities, emphasizing the importance of including microscopic absorption cross-sections $$\sigma_{X}$$ and $$\sigma_{Y}$$ in the calculations. The final formula presented is $$\Sigma_{mix}= \frac{No\ of\ X\ atoms}{Volume\ of\ X} \times \frac{Volume\ of\ X}{Volume\ of\ X+Y} \times \sigma_{X} + \frac{No\ of\ Y\ atoms}{Volume\ of\ Y} \times \frac{Volume\ of\ Y}{Volume\ of\ X+Y} \times \sigma_{Y}$$, which correctly accounts for the dimensions and units involved.
PREREQUISITES
- Understanding of macroscopic and microscopic cross-sections in nuclear engineering.
- Familiarity with number density concepts and their applications in mixtures.
- Knowledge of volume fractions and their significance in physical calculations.
- Basic grasp of dimensional analysis in physics.
NEXT STEPS
- Study the derivation of macroscopic cross-sections in nuclear reactions.
- Learn about the role of microscopic cross-sections in neutron transport theory.
- Explore the concept of number density in multi-component systems.
- Investigate dimensional analysis techniques for verifying physical equations.
USEFUL FOR
Nuclear engineers, physicists, and students studying nuclear engineering concepts, particularly those focused on cross-section calculations and mixture properties.