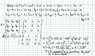Obtain the extremum of f(x,y,z)

[s3a]

Homework Statement

Obtain the extremum of f(x,y,z) = 2x^2 + y^2 + 2z^2 + 2xy + 2xz + 2y + x - 3z - 5 and determine its nature.

Homework Equations

Partial differentiation and systems of equations.

The Attempt at a Solution

My attempt is attached. In addition to confirming if what I did so far is correct, I would appreciate it if someone could also tell me how to "find the nature" of the point. I believe that means to state if it's a minimum, maximum or saddle point. For a function of two variables, I would know what to do but for a function of three variables, I do not. I remember hearing that we are not responsible for figuring out the nature of points higher than two variables using the method I would use which is the [f_(xy)]^2 - f_(xx) * f_(yy) test but that we should be able to do such a problem using a different easier method. I'm in a Calculus 3 course.

Any help would be greatly appreciated!
Thanks in advance!

 

[HallsofIvy]

You have $f(x,y,z)= 2x^2+ y^2+ 2z^2+ 2xy+ 2xz+ 2yz+ x- 3z- 5$
and assert that $f_x= 4x+ 2y+ 2z+ 2y+ 1$
Where did that second "2y" come from?

The other two derivatives are correct.

As for determining what kind of extremum, there are two things you can do. The most basic is to look at values around the (x,y,z) point you get. Since there is only the one extremum, if other values of (x,y,z) give smaller values for f, you have a maximum, if higher, a minimum. Of course, there is the possibility of a saddle point but since the problem asks for an "extremum" that shouldn't happen.

More sophisticated is to form the matrix of second derivatives:
$$\begin{bmatrix}f_{xx} & f_{xy} & f_{xz} \\ f_{yx} & f_{yy} & f_{yz} \\ f_{zx} & f_{zy} & f_{zz}\end{bmatrix}$$
evaluated at the critical point.

Because of the equality of the "mixed" derivatives, $f_{xy}= f_{yx}$, etc., that is a symmetric matrix and so has all real eigenvalues. If all eigenvalues are positive the extremum is a minimum, if all eigenvalues are negative, it is a maximum, and if there are both positive and negative eigenvalues, there is no "exteremum" but a saddle point.

 

[s3a]

Thank you for the informative reply.

By visual inspection, I don't think I did anything wrong but I get f_(xy) != f_(yx).

Before I proceed, could you please just check if I did something wrong and explain why I get f_(xy) != f_(yx) whether my work is correct or not?

 

[s3a]

I just realized that I did f_(xx) != f_(yy).

Sorry.

 

[s3a]

Let's call that matrix you gave me H for Hessian.

Is my latest attachment 100% correct?