Undergrad What is the proper format for solving this ODE using an Excel add-in calculator?

[jknight291]

I am attempting to solve an ODE using a Calculus add-in for Excel. I am an industry professional and I have not even thought about Differential Equations in 8 years. The equation that I am attempting to solve is in the form:

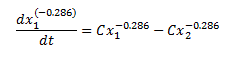(1)

The ODE solver that I am using solves equations of the form:

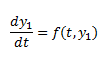(2)

The results that I get by solving equation 1 above using my Excel Add-in for ODEs is a sinusoidal type reaction. However, when I solve numerically I get the expected result.

I think my ODE solver may be solving for

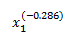and not just x`1. I tried to transform the results using algebra but the results were still obscure.

I think I may need to transform equation 1 to match the format of equation 2 before solving, but I am not sure. Like I said, it has been several years since taking a DE course so I am little rusty.

Can anyone offer some help?

Thanks!

 

[Gaussian97]

What is $x_2$?

 

[jknight291]

A nonlinear algebraic equation. I am solving this as a system of equations.

 

[pasmith]

To echo @Gaussian97,

What is x_2? Is it a constant? Is it a known function of time? Is there another ODE which governs its evolution over time?

If the ODE solver expects an equation of the form \dot y = f(t,y) then you will need to put your ODE into that form before solving. Now by the chain rule <br /> \frac{dx_1^{-0.286}}{dt} = -{0.286}x_1^{-1.286}\frac{dx_1}{dt} so <br /> \frac{dx_1}{dt} = -\frac{x_1^{1.286}}{0.286}C(x_1^{-0.286} - x_2^{-0.286}).