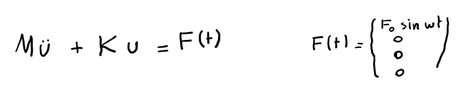ODE solver for second Order ODE with Stiffness and Mass Matrices

[ihebmtir]

TL;DR

i have encoutered this Problem where i need to solve an ordinary differential Equation using ODE45 for M*u''+K*u=f(t)

i am new to MATLAB and and as shown below I have a second order differential equation M*u''+K*u=F(t) where M is the mass matrix and K is the stifness matrix and u is the displacement.
and i have to write a code for MATLAB using ODE45 to get a solution for u. there was not so much information on how to solve an ODE that´'s written on Matrix form, i would be really thankful for you help

 

[Dr.D]

Do you have a definition for the vector {f(t)}?

 

[ihebmtir]

yes F(t)=[F0*sin(w*t), 0, 0, 0]
and Both M and K are 4X4 Matrices

 

[onatirec]

Obviously you will need some initial conditions as well. I will attach a similar example problem and solution code.

It can be a little tricky getting the code to run. You should save the lower function in a separate script (called "f" in this case - since that's what the ode45 function calls) in the working folder. The upper part is what you will run and it calls the other function. There's probably a more elegant way of doing it, but I don't know it.

xo=[0; 0.1; 1; 0];
ts=[0 20];
[t,x]=ode45('f',ts,xo);
plot(t,x(:,1),t,x(:,2),'--')
%------------------------------------------
function v=f(t,x)
M=[2 0; 0 1];
C=[3 -0.5; -0.5 0.5];
K=[3 -1; -1 1];
B=[1; 1];
w=2;
A1=[zeros(2) eye(2); -inv(M)*K -inv(M)*C];
f=inv(M)*B;
v=A1*x+[0;0; f]*sin(w*t);