On the application of the goodman equation to a multiaxial stress state

[Whitebread]

I don't quite understand how the modified goodman equation can be applied to a multiaxial stress state. The explanation given in my stress analysis class has been quite confusing and verbose so I've come here to see if I can't get a better understanding.

First I'll lay out what I think to be true:

Utilizing the Von-Mises failure criterion in place of the uni-axial stresses in the goodman equation should be able to account for a multiaxial stress state AND fatigue. Here's how I think it should work

Uni-axial stress amplitude is replaced with von-mises stress amplitude (same equation, different stresses)

The fatigue limit at whatever number of cycles the designer is concerned with is replaced with the Von-Mises stress at that stress amplitude. Or: (Uni-Axial Fatigue limit at X cycles)*(1/3)=fully reversed stress amplitude (or SIGMAar in the good man equation).

Mean stress is replaced with mean von-mises stress (same equation, different stresses)

Ultimate stress is replaced with (sqrt(2)/3)*SIGMA(u) or the von mises stress at failure.

Equations:

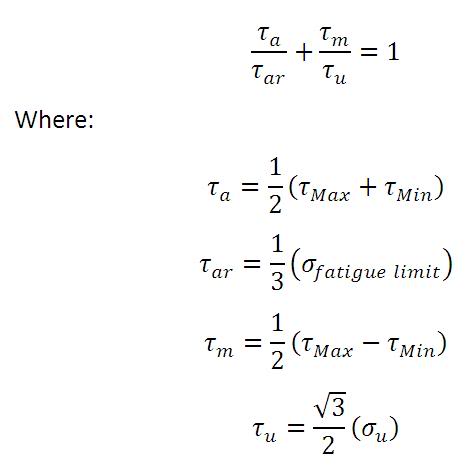
That last equation should be sqrt(2)/3. Made a mistake when writing the equations. Thanks.
Is this correct?

 

[binoyjjohn]

Actually you got the equations for stress amplitude (tau_a) and mean stress (tau_m) swapped, here.

 

[nvn]

Whitebread wrote:[/color] "Utilizing the von Mises failure criterion in place of the uniaxial stresses in the [modified] Goodman equation should be able to account for a multiaxial stress state and fatigue. Here's how I think it should work. Uniaxial stress amplitude is replaced with von Mises stress amplitude."[/color]

Agreed.

Whitebread wrote:[/color] "The fatigue limit at whatever number of cycles the designer is concerned with is replaced with the von Mises stress at that stress amplitude. Or, (uniaxial fatigue limit at N cycles)*(1/3) = fully reversed stress amplitude (or sigma_ar in the [modified] Goodman equation)."[/color]

Disagree. Fatigue strength is a material property, not a von Mises stress. The fatigue strength should not be adjusted.

Whitebread wrote:[/color] "Mean stress is replaced with mean von Mises stress."[/color]

Agreed.

Whitebread wrote:[/color] "Ultimate stress is replaced with (sqrt(2)/3)*sigma_u, or the von Mises stress at failure."[/color]

Disagree. Tensile ultimate (mean) strength, Stu, is a material property, not a von Mises stress, and should not be adjusted.

A similar question is posted at thread https://www.physicsforums.com/showthread.php?t=304749" .

 

[Whitebread]

Well its been a while. Since I posted and the project I posted it for was long since been turned in. Thanks for the input and the link though. Its quite helpful since this information just doesn't seem to be recorded anywhere.