Open and Closed Sets .... Conway, Example 5.3.4 (b) .... ....

[Math Amateur]

TL;DR

The thread concerns the use of the reverse triangle inequality to prove that an open ball is an open set ...

I am reading John B. Conway's book: A First Course in Analysis and am focused on Chapter 5: Metric and Euclidean Spaces ... and in particular I am focused on Section 5.3: Open and Closed Sets ...

Conway's Example 5.3,4 (b) reads as follows ... ...

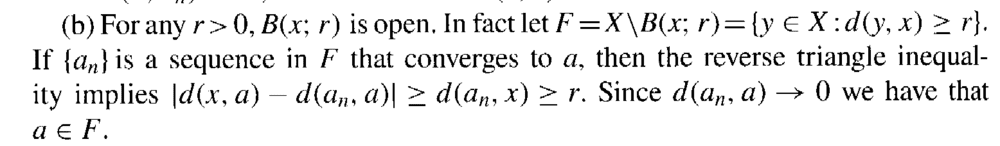
Note that Conway defines open and closed sets as follows:

Now ... in the text of Example 5.3.4 shown above we read the following:

" ... ... the Reverse Triangle Inequality implies $\mid d(x,a) - d( a_n, a ) \mid \ge d(a_n, x) \ge r$ ... ... "Can someone please explain to me exactly why $\mid d(x,a) - d( a_n, a ) \mid \ge d(a_n, x) \ge r$ ...

My thoughts on this are as follows ...

It seems to me that the Reverse Triangle Inequality implies $\mid d(x,a) - d( a_n, a ) \mid \le d(a_n, x)$ ... ?Hope someone can clarify the above issue ...

Peter===================================================================================The above post mentions the Reverse Triangle Inequality ... Conway's statement of that inequality is as follows:

Hope that helps ..

Peter

 

[member 587159]

I think it is a mistake. Indeed, the reverse triangle inequality is the other way around. I don't see a way to save the proof, so I can only offer some alternative proofs. The first is elementary, the second uses the topological definition of continuity, and the third one is probably the proof the author had in mind:

Way 1: Use that a set is open iff all its points are interior points.

Let $x \in B(a,r)$. We prove that $x$ is an interior point of this ball. By assumption, we have $d(x,a) < r$ and thus $\epsilon := r-d(x,a) > 0$.

Exercice for you: show that $B(x,\epsilon) \subseteq B(a,r)$. This will show that $x$ is indeed an interior point.

Way 2: Prove that the map $\psi: x \mapsto d(a,x)$ is continuous (here you can use the reverse triangle inequality ;))

Then observe that $B(a,r) = \psi^{-1}(]-\infty, r[)$ is open, as inverse image of an open set under a continuous map.

Way 3: To prove $B(a,r)$ is open, we show that $X\setminus B(a,r)$ is closed using your definition.

So, let $x_n \to x$ and $x_n \in B(a,r)$ for all $n$. Thus $d(a,x_n) \geq r$ for all $n$.

Now, by the reverse triangle inequality we have

$$|d(a,x_n)-d(x,a)| \leq d(x_n,x) \to 0$$

Thus $\lim_{n \to \infty} d(a,x_n) = d(x,a)$

By taking limits on both sides of the inequality $d(a,x_n) \geq r$, it follows that $d(a,x) \geq r$. Thus $x \in X \setminus B(a,r)$.

Choose the proof you prefer :)

 

[soloenergy]

Hello Peter,

The Reverse Triangle Inequality is a property of metric spaces, which are sets with a distance function defined between elements. In this case, the elements are points in a metric space and the distance function is denoted by d(a,b) where a and b are points in the space.

The Reverse Triangle Inequality states that for any three points a, b, and c in a metric space, the following inequality holds:

|d(a,c) - d(b,c)| ≤ d(a,b)

In the context of Example 5.3.4, we have four points: x, a, an, and a. The distance between x and a is d(x,a), the distance between an and a is d(an,a), and the distance between an and x is d(an,x). Using the Reverse Triangle Inequality, we can rewrite the inequality as:

|d(x,a) - d(an,a)| ≤ d(x,an)

Since we know that d(an,a) = r, we can substitute this into the inequality to get:

|d(x,a) - r| ≤ d(x,an)

This is the same as saying:

d(x,a) - r ≤ d(x,an) and d(x,a) + r ≥ d(x,an)

Combining these two inequalities, we get:

d(x,a) - r ≤ d(x,an) ≤ d(x,a) + r

This is the same as saying:

|r - d(x,a)| ≤ d(x,an) ≤ r + d(x,a)

Since the distance between two points cannot be negative, we can remove the absolute value and rewrite the inequality as:

d(x,a) - d(an,a) ≤ d(x,an) ≤ d(x,a) + d(an,a)

This is the same as saying:

|d(x,a) - d(an,a)| ≤ d(x,an) ≤ d(x,a) + d(an,a)

Which is the same as:

|d(x,a) - d(an,a)| ≤ d(x,an) ≤ d(x,a) + d(an,a)

This is the same as:

|r - d(x,a)| ≤ d(x,an) ≤ r + d(x,a)

Finally, we can substitute in d(an,a) = r to get:

|r - d(x,a)| ≤ d(x,an) ≤ r + d(x,a)

Which is the same as:

|r - d(x,a)| ≤