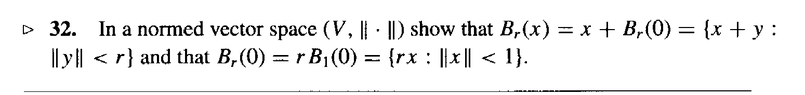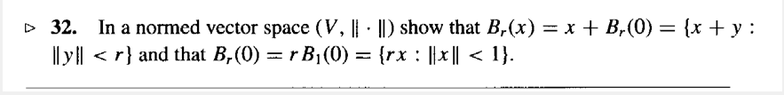Open Balls in a Normed Vector Space .... Carothers, Exercise 32

[Math Amateur]

I am reading N. L. Carothers' book: "Real Analysis". ... ...

I am focused on Chapter 3: Metrics and Norms ... ...

I need help Exercise 32 on page 46 ... ... Exercise 32 reads as follows:

View attachment 9201
I have not been able to make much progress ...

We have ...\(\displaystyle B_r(x) = \{ y \in M \ : \ d(x, y) \lt r \}\)

... and ...

\(\displaystyle B_r(0) = \{ y \in M \ : \ d(0, y) \lt r \}\)... and ...\(\displaystyle x + B_r(0) = x + \{ y \in M \ : \ d(0, y) \lt r \}\)But ... how do we formally proceed from here ...
Hope that someone can help ...

Peter===================================================================================

The above post refers to/involves the notion of an open ball ... so I am providing Carothers' definition of the same ... as follows:
View attachment 9202
The above post also refers to/involves the notion of a normed vector space ... so I am providing Carothers' definition of the same ... as follows:
View attachment 9203
View attachment 9204Hope that helps ...

Peter

 

[Opalg]

Given $x,y\in V$, let $z = y-x$. Then $$y \in B_r(x) \Longrightarrow \|y-x\|<r \Longrightarrow \|z\|<r \Longrightarrow z\in B_r(0) \Longrightarrow y = x+z \in x + B_r(0).$$ Therefore $B_r(x) \subseteq x + B_r(0)$. That argument also works in the opposite direction, giving the reverse inclusion in the same way.

 

[Math Amateur]

Given $x,y\in V$, let $z = y-x$. Then $$y \in B_r(x) \Longrightarrow \|y-x\|<r \Longrightarrow \|z\|<r \Longrightarrow z\in B_r(0) \Longrightarrow y = x+z \in x + B_r(0).$$ Therefore $B_r(x) \subseteq x + B_r(0)$. That argument also works in the opposite direction, giving the reverse inclusion in the same way.

Hi Opalg ...

Thanks for the help ...

... but ... just a clarification ...

You write:

" ... ... \(\displaystyle z\in B_r(0) \Longrightarrow y = x+z \in x + B_r(0)\) ... ... "I am somewhat perplexed as to how we justify (or even interpret ...) the above statement ... how do you justify it based solely on the axioms of a normed vector space and the basics of set theory ... indeed ... what does the statement ... ... \(\displaystyle y = x+z \in x + B_r(0)\) ... ... mean exactly ...
My thoughts are as follows ...

\(\displaystyle y = x + z\)

\(\displaystyle \Longrightarrow y = x \ + \) ... a particular element of the set \(\displaystyle B_r(0)\)

\(\displaystyle \Longrightarrow\) ... (means ... ) ... \(\displaystyle y \in x + B_r(0)\)Is that correct ... am I interpreting things correctly ...?

Regarding the reverse argument ... my thoughts are as follows:

\(\displaystyle y \in x + B_r(0)\)

\(\displaystyle \Longrightarrow y = x + z \) where \(\displaystyle z \in B_r(0)\)

\(\displaystyle \Longrightarrow y - x = z\) where \(\displaystyle z \in B_r(0)\)But \(\displaystyle \| z \| \lt r\)

\(\displaystyle \Longrightarrow \| y - x \| \lt r\)

\(\displaystyle \Longrightarrow y \in B_x(r)\) Is that correct?Hope you can help further ...

Peter

 

[Opalg]

You write:

" ... ... \(\displaystyle z\in B_r(0) \Longrightarrow y = x+z \in x + B_r(0)\) ... ... "I am somewhat perplexed as to how we justify (or even interpret ...) the above statement ... how do you justify it based solely on the axioms of a normed vector space and the basics of set theory ... indeed ... what does the statement ... ... \(\displaystyle y = x+z \in x + B_r(0)\) ... ... mean exactly ...
My thoughts are as follows ...

\(\displaystyle y = x + z\)

\(\displaystyle \Longrightarrow y = x \ + \) ... a particular element of the set \(\displaystyle B_r(0)\)

\(\displaystyle \Longrightarrow\) ... (means ... ) ... \(\displaystyle y \in x + B_r(0)\)Is that correct ... am I interpreting things correctly ...?

That is correct. In fact, in the statement of Exercise 32, Carothers defines $x+B_r(0)$ to mean $\{x+y:\|y\|<r\}$:
View attachment 9205

Regarding the reverse argument ... my thoughts are as follows:

\(\displaystyle y \in x + B_r(0)\)

\(\displaystyle \Longrightarrow y = x + z \) where \(\displaystyle z \in B_r(0)\)

\(\displaystyle \Longrightarrow y - x = z\) where \(\displaystyle z \in B_r(0)\)But \(\displaystyle \| z \| \lt r\)

\(\displaystyle \Longrightarrow \| y - x \| \lt r\)

\(\displaystyle \Longrightarrow y \in B_x(r)\) Is that correct?

For the reverse inclusion $x+B_r(0) \subseteq B_r(x)$, you need to start with an element $z\in B_r(0)$. Then $$z\in B_r(0) \Longrightarrow \|z\|<r \Longrightarrow \|x-(x+z)\|<r \Longrightarrow x+z\in B_r(x).$$

 

[Math Amateur]

That is correct. In fact, in the statement of Exercise 32, Carothers defines $x+B_r(0)$ to mean $\{x+y:\|y\|<r\}$:
For the reverse inclusion $x+B_r(0) \subseteq B_r(x)$, you need to start with an element $z\in B_r(0)$. Then $$z\in B_r(0) \Longrightarrow \|z\|<r \Longrightarrow \|x-(x+z)\|<r \Longrightarrow x+z\in B_r(x).$$

Thanks Opalg ...

Still thinking over the reverse inclusion proof ...

Peter