Sebastian Martinez
- 11
- 0
Homework Statement
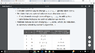
I can't understand why cashier's algorithm is optimal for U.S coins: 1, 5,10,25,100
Homework Equations
The Attempt at a Solution
The way cashier's algorithm works is that you pick the denomination of closest value to the expected amount. I am trying to read a lot of slides but it's not clear. One key point to understand is that each denomination is a multiple of the previous denomination, but what does that tell me about its optimality?... I am trying to understand the attached table
Attachments
Last edited: