Optimization of barrel length in pneumatic cannons

[Juanda]

TL;DR Summary

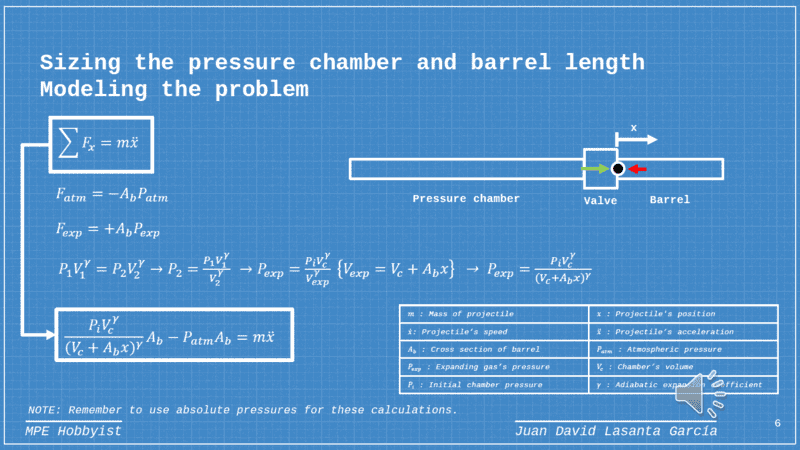
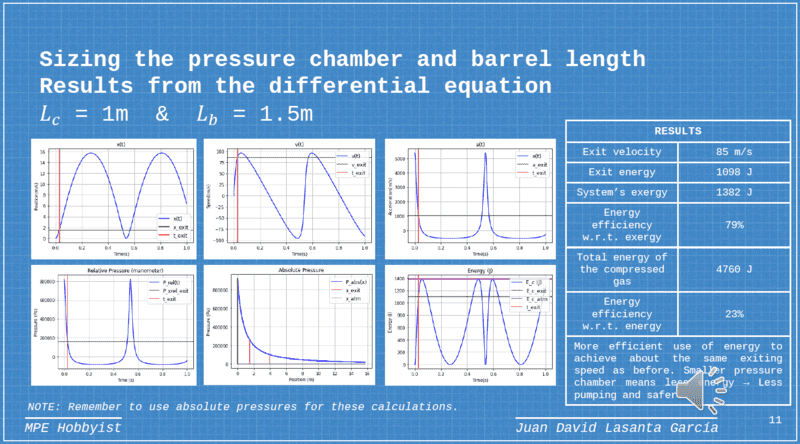
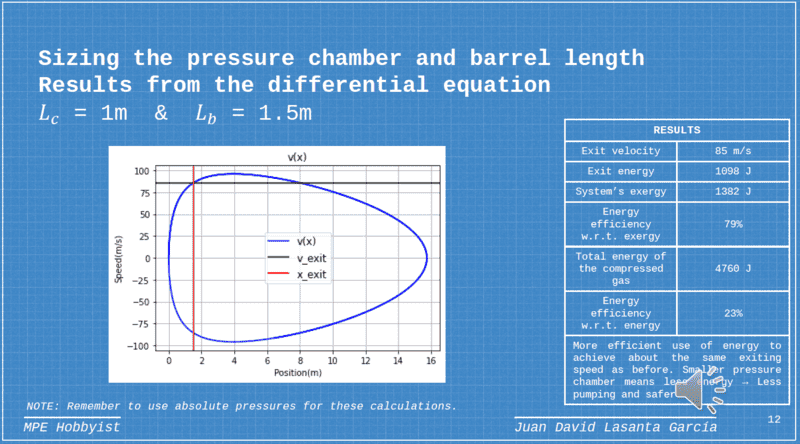
Derivation of the optimum ratio for the volume chamber and the cannon chamber.

I was checking bait cannons and potato guns on the internet because they are fun. Maybe one day I'll build my own.

First of all, these cannons use multiple sources of energy (combustion using hair spray, dry ice, etc.). I'll just consider compressed air cannons because I think they are the most reliable option.

There are plenty of videos detailing the process to make them but I couldn't find much information about what size you should make the barrel for a given pressure chamber. Some people provide rules of thumb for it or experiments for a given cannon and things like that. I tried to solve the generic math to be able to adapt it to any size.

I created a PPT with the analysis.


Some people prefer reading because it's faster so I attached the slides too as a PDF.

As a summary, here are a few key slides:

1. Do you see any fundamental errors in the derivation?
2. How far away from reality do you think are the simplifications?
   1. Ideal gas behavior
   2. Adiabatic expansion
   3. No friction
   4. Perfect seal
   5. Instantaneous valve opening time
3. Would you model the system differently?
4. Since the energy in the system comes from the internal energy in the ideal gas, through energy conservation I should be able to find the exiting velocity with $\Delta U_i=m_{air}c_v\Delta T$. However, at no point, I defined the temperature of the gas or the amount of gas present. I feel I should be able to obtain all the information about the gas with the given data but I'm missing how.
5. From the equations, I could technically achieve supersonic speeds by either increasing the initial pressure or the size of the pressure chamber. However, I am pretty sure that is not how it works. Do you recommend any particular book to be able to understand that scenario? Is it possible to get away with this while using regular air and simple geometries? It's not like I'm going to build such a thing but it'd be cool to consider the case.

I hope you found that interesting and maybe we can have some cool conversations about it.

 

[Bystander]

https://en.wikipedia.org/wiki/Punkin_chunkin

 

[Frabjous]

Here’s a readable paper.
http://persweb.wabash.edu/facstaff/madsenm/publications/AJP_80_24_rohrbach_air_cannon.pdf
For the high velocity regime, you also have to take into account that the gas has kinetic energy so that it can keep up with the projectile.

 

[Juanda]

https://en.wikipedia.org/wiki/Punkin_chunkin

I think only the USA could host an event like that

 

[Juanda]

Here’s a readable paper.
http://persweb.wabash.edu/facstaff/madsenm/publications/AJP_80_24_rohrbach_air_cannon.pdf
For the high velocity regime, you also have to take into account that the gas has kinetic energy so that it can keep up with the projectile.

I just read the paper. It's a very interesting read. It shows how at some point it is necessary to rely on a combination of theory and experimental data to be able to model complex systems.
One of the assumptions I did was that the valve is perfect so there is no pressure differential across it. These guys went all in, made the equations, and found the characteristics of the valve $r_{max}$ and $C_v$ from the results when firing the cannon.

The only point I'm missing from the paper to fully hit the mark is the optimization of the barrel length for a given pressure. It would be necessary to study if the initial conditions choke the valve or not in order to know which formula for $Q$ should be used.

Since they are choking the valve I assume there is plenty of energy left in that compressed air to keep accelerating the projectile. My main interest in optimizing this aspect of the cannon is because being efficient usually pays off. There is no point in increasing the pressure or volume of the chamber if that energy doesn't end up in the projectile. Especially if this needs to be pumped by hand with something like a bike pump because it'd take more time and effort.

By the way, was the paper hard to find? Whenever I search for papers related to any topic I never find what I'm really looking for.

 

[erobz]

Didn’t read the paper, but the projectile is going to set up a pressure differential from itself to the end of the barrel via the viscosity of the flow( unsteady)resulting on a larger than atmospheric pressure on the front of the projectile, and the projectile will also experience drag from kinetic friction in the barrel. Those will be parameterized by the length of the barrel(at least the back pressure will). I didn’t see that in the slides presented. I think the optimization you are looking for is tied to those quantifiable relationships. At least that is where I would look.

If the flow velocity is near Mach 0.3 you’ll probably need to account for compressible flow behavior.

 

[Juanda]

Didn’t read the paper, but the projectile is going to set up a pressure differential from itself to the end of the barrel via the viscosity of the flow( unsteady)resulting on a larger than atmospheric pressure on the front of the projectile, and the projectile will also experience drag from kinetic friction in the barrel. I didn’t see that in the slides presented. I think the optimization you are looking for is tied to those quantifiable relationships. At least that is where I would look.

If the flow velocity is near Mach 0.3 you’ll probably need to account for compressible flow behavior.

Friction will definitely play a role. This is why I didn't push the optimization all the way to the top of the curve.
Friction will flatten and displace that curve to the left so I left the exiting conditions with an 80% efficiency as an approximation.

If I'm understanding you correctly you're saying the forces on the projectile will be:
$\sum F=m\ddot{x}\rightarrow P_{exp}A-P_{atm+comp}A-\mu N-c\dot{x}=m\ddot{x}$

• For $P_{exp}$ I could get a more realistic value through experimentation as stated on the paper @Frabjous shared here. That would take into account the inefficiencies of the valve although it still considers it opens infinitely fast.
• For $P_{atm+comp}$ you are saying that just the atmospheric pressure is not enough because as the projectile approaches Mach 0.3 there will be a greater pressure at the front. I understand the concept but I have no clue on how I could calculate that. That's why I only used $P_{atm}$.
• For $\mu N$ it can be ignored as long as the projectile doesn't have a hard fit in the barrel and the friction coefficient is low enough. For example, in bait cannons people shoot blocks of ice that slide through the barrel with little clearance.
• For $c\dot{x}$, the values of c are typically defined for open space conditions. For example, a ball traveling through the air. However, I didn't find information about $c$ for a traveling projectile inside a barrel. Also, I am assuming that $c$ depends on the velocity of the projectile and the pressure in front of it. Again, I don't really know how to calculate that.

 

[erobz]

Friction will definitely play a role. This is why I didn't push the optimization all the way to the top of the curve.
Friction will flatten and displace that curve to the left so I left the exiting conditions with an 80% efficiency as an approximation.
View attachment 328189

If I'm understanding you correctly you're saying the forces on the projectile will be:
$\sum F=m\ddot{x}\rightarrow P_{exp}A-P_{atm+comp}A-\mu N-c\dot{x}=m\ddot{x}$

• For $P_{exp}$ I could get a more realistic value through experimentation as stated on the paper @Frabjous shared here. That would take into account the inefficiencies of the valve although it still considers it opens infinitely fast.
• For $P_{atm+comp}$ you are saying that just the atmospheric pressure is not enough because as the projectile approaches Mach 0.3 there will be a greater pressure at the front. I understand the concept but I have no clue on how I could calculate that. That's why I only used $P_{atm}$.

You are trying to optimize the length of the barrel. So, the work done by the expanding gas must accelerate the projectile and the air in the barrel in front of it. The air in front of projectile( inside the barrel ) will have a pressure gradient established from two effects as far as I can tell that are going to work against accelerating the projectile.

1) The gas itself will compress in front of the projectile purely because it is accelerating. The mass ahead of the projectile will be a function of the length of the barrel and time.

2) The mass in the barrel ahead of the projectile will be experiencing viscous forces proportional to $\dot x$ acting on it. As in above the mass will be a function of length of the barrel and time.

• For $\mu N$ it can be ignored as long as the projectile doesn't have a hard fit in the barrel and the friction coefficient is low enough. For example, in bait cannons people shoot blocks of ice that slide through the barrel with little clearance.

I would include a constant frictional force. Computationally it’s not a significant complexity. We are certainly already in the domain of numerical solution methodology. Also, if you’ve fired a potato they are forced into the barrel, I’m not sure it’s an insignificant force if you want a reasonably good seal.

If all these effects are small, then what is left to optimize?

I would try to approach it from a work energy standpoint. It’s likely going to be complex any way you try to cut it, but you have to end up with some competing forces that are a function of $l-x$ if you hope to optimize for $l$?

 

[Juanda]

If all these effects are small, then what is left to optimize?

Even in a world without friction and imperfections, the length of the barrel can be optimized and it's got a big impact on performance. As shown in the slides, the pressure pushing the projectile decreases as it moves forward. Then, it is optimal to cut the barrel at the point where the pressure pushing the ball is equal to the pressure in front of the ball. If the barrel is longer than that the pressure in front of the projectile will be greater so the projectile will slow down. That is why in the simulation you can see a periodic movement of the projectile.
Since for the simulation I ignored all kinds of imperfections, I would cut the barrel a little earlier than the math suggests.

I would try to approach it from a work energy standpoint. It’s likely going to be complex any way you try to cut it, but you have to end up with some competing forces that are a function of $l-x$ if you hope to optimize for $l$?

I initially thought about using $\Delta U_i=m_{air}c_v\Delta T$ because I assumed an adiabatic expansion but if I ever build this I won't have as much control over the temperature. I'll have a pressure gauge instead and the volumes are known so that's why I optimized it like this. I assume it must also be possible to do it using energy but I felt this method was more convenient.

 

[erobz]

Even in a world without friction and imperfections, the length of the barrel can be optimized and it's got a big impact on performance. As shown in the slides, the pressure pushing the projectile decreases as it moves forward. Then, it is optimal to cut the barrel at the point where the pressure pushing the ball is equal to the pressure in front of the ball. If the barrel is longer than that the pressure in front of the projectile will be greater so the projectile will slow down. That is why in the simulation you can see a periodic movement of the projectile.
Since for the simulation I ignored all kinds of imperfections, I would cut the barrel a little earlier than the math suggests.

Oh, I see what you are saying. You almost certainly don’t want it to expand to sub atmospheric pressures before the projectile leaves the barrel.

 

[erobz]

The question that I have then is does that preclude (accounting for everything else mentioned ) there is an optimum at a shorter barrel length?

 

[Juanda]

The question that I then have is does that then preclude that accounting for everything else mentioned there is an optimum at a shorter barrel length?

I'm having trouble processing the question.
Are you asking if there is a second optimum barrel length that's shorter than the one I found?
There isn't according to the model I derived (adiabatic expansion, perfect world, no friction, etc).
The red dot shows the optimum length for the barrel (~4m) for which the exit velocity of the projectile would peak.

However, for the design I chose the point defined by the black and red lines (1.5m long barrel) because friction and other imperfections will shift and flatten that curve and I imagined the cannon as a portable item so the size must be manageable. For such dimensions, initial pressure, chamber size, no imperfections and so on, the efficiciecy with respect to the exergy of the system is 80%.

Let me know if that's not what you meant with your question.

 

[erobz]

I'm having trouble processing the question.
Are you asking if there is a second optimum barrel length that's shorter than the one I found?

Yeah, when accounting for viscous effects, kinetic friction, and the kinetic energy of the flow, is there is a shorter optimum barrel… is what I’m expecting.

 

[Juanda]

Yeah, when accounting for viscous effects, kinetic friction, and the kinetic energy of the flow

I would assume not. I'm pretty sure that graph would be transformed into something like this.

So the energy is being dissipated but I assume the overall shape remains although flattened and shifted to the left.
I don't know how to implement all the forces you mention but I can add something like the dynamic friction with the barrel as a constant opposing the movement and the viscous form as $-c \dot{x}$ using arbitrary values for $\mu$ and $c$.

I will simulate it tomorrow with those new forces to confirm the hypothesis though.

 

[erobz]

I would assume not. I'm pretty sure that graph would be transformed into something like this.

View attachment 328202

So the energy is being dissipated but I assume the overall shape remains although flattened and shifted to the left.
I don't know how to implement all the forces you mention but I can add something like the dynamic friction with the barrel as a constant opposing the movement and the viscous form as $-c \dot{x}$ using arbitrary values for $\mu$ and $c$.

I will simulate it tomorrow with those new forces to confirm the hypothesis though.

If you assume constant pressure ahead of the projectile, (which is not consistent with the effects of the viscous term $-c\dot x$), there will be also be a $\rho A( l-x) \ddot x$ term. The density is not constant ahead of the projectile along the remains length of barrel (neither is the velocity), but to put a flag in the sand pile let’s say it is. Even though the mass is relatively small and diminishing, the accelerations are relatively high. It’s not clear to me that it’s immediately negligible.

 

[Juanda]

I would assume not. I'm pretty sure that graph would be transformed into something like this.

View attachment 328202

So the energy is being dissipated but I assume the overall shape remains although flattened and shifted to the left.
I don't know how to implement all the forces you mention but I can add something like the dynamic friction with the barrel as a constant opposing the movement and the viscous form as $-c \dot{x}$ using arbitrary values for $\mu$ and $c$.

I will simulate it tomorrow with those new forces to confirm the hypothesis though.

I did simulate it again. This time following this formula:
$\sum F=m\ddot{x}\rightarrow P_{exp}A-P_{atm}A-\mu N-c\dot{x}=m\ddot{x}$

This is the resulting graph:
$\mu N = 50$ and $c=2$

As initially hypothesized, there is no additional optimal point for the barrel length.

As a side note, since I didn't implement the necessary conditionals to capture the transition from dynamic friction to static friction, the simulation starts doing all kinds of wacky things when the projectile reaches points with 0 velocities.

Adding that behavior is a rather tedious task but, in this case, it adds no value since we're interested in cutting the barrel (hence cutting the simulation) at the point where the projectile reaches peak velocity (vertical red line).

If I make $\mu = 0$ which could be a fairly good approximation depending on the projectile characteristics and comparison with the rest of the forces involved, the resulting graphs are smoother and the neutral point approaches the $x \approx 4m$ at the barrel where the pressure is equal on both sides of the projectile (1 atm).

Comparing that with the original curve it can be seen how, although the overall shape is maintained, the curve is flattened (slower speeds reached) and shifted to the left (peak velocity does no longer happen at the point of equal pressures on both sides $x \approx 4m$).

If you assume constant pressure ahead of the projectile, (which is not consistent with the effects of the viscous term $-c\dot x$), there will be also be a $\rho A( l-x) \ddot x$ term. The density is not constant ahead of the projectile along the remains length of barrel (neither is the velocity), but to put a flag in the sand pile let’s say it is. Even though the mass is relatively small and diminishing, the accelerations are relatively high. It’s not clear to me that it’s immediately negligible.

I believe the force due to the inertia of the pushed gas in front of the barrel will be very small so it won't affect much. The paper supplied by @Frabjous at #3 seems to agree with this. They didn't add that force acting on the projectile and the experimental data shows a good fit (at least for the speed range shown).

They considered $f=0$ so the only acting forces are due to the difference in pressures. Also, they considered the pressure in front of the projectile to be constant. Here you can see the results they obtained for 3 different projectiles.

The main difference between my original model and theirs is that they considered the physical limitations of the valve while I simply used the adiabatic expansion of the gas. I would like to take my analysis to the next level and include that as well but I would need to go through some experimentation to characterize the valve that such a cannon would use. Due to a lack of equipment, I'll have to settle with only the mathematical results.

 

[erobz]

I did simulate it again. This time following this formula:
$\sum F=m\ddot{x}\rightarrow P_{exp}A-P_{atm}A-\mu N-c\dot{x}=m\ddot{x}$

This is the resulting graph:
$\mu N = 50$ and $c=2$
View attachment 328231

As initially hypothesized, there is no additional optimal point for the barrel length.

As a side note, since I didn't implement the necessary conditionals to capture the transition from dynamic friction to static friction, the simulation starts doing all kinds of wacky things when the projectile reaches points with 0 velocities.
View attachment 328235
View attachment 328232

Adding that behavior is a rather tedious task but, in this case, it adds no value since we're interested in cutting the barrel (hence cutting the simulation) at the point where the projectile reaches peak velocity (vertical red line).

If I make $\mu = 0$ which could be a fairly good approximation depending on the projectile characteristics and comparison with the rest of the forces involved, the resulting graphs are smoother and the neutral point approaches the $x \approx 4m$ at the barrel where the pressure is equal on both sides of the projectile (1 atm).
View attachment 328233

Comparing that with the original curve it can be seen how, although the overall shape is maintained, the curve is flattened (slower speeds reached) and shifted to the left (peak velocity does no longer happen at the point of equal pressures on both sides $x \approx 4m$).
View attachment 328234

I believe the force due to the inertia of the pushed gas in front of the barrel will be very small so it won't affect much. The paper supplied by @Frabjous at #3 seems to agree with this. They didn't add that force acting on the projectile and the experimental data shows a good fit (at least for the speed range shown).
View attachment 328236
They considered $f=0$ so the only acting forces are due to the difference in pressures. Also, they considered the pressure in front of the projectile to be constant. Here you can see the results they obtained for 3 different projectiles.
View attachment 328237

The main difference between my original model and theirs is that they considered the physical limitations of the valve while I simply used the adiabatic expansion of the gas. I would like to take my analysis to the next level and include that as well but I would need to go through some experimentation to characterize the valve that such a cannon would use. Due to a lack of equipment, I'll have to settle with only the mathematical results.

They say they performed a manual 2 parameter fit ( the black lines) the models in their own estimation significantly overshoot the exit velocity due to the missing quadratic drag term. I think it is not quadratic drag (exactly), but is instead that atmospheric pressure acting on the leading face of the projectile is not such a good approximation. I think the flow characteristics ahead of the projectile are important. They are what set up the pressure differential across the barrel between the leading face of the projectile and the exit. Solving for that precisely is almost certainly another ball game. I think I have an idea on how to rough it though.

 

[Juanda]

They say they performed a manual 2 parameter fit ( the black lines) the models in their own estimation significantly overshoot the exit velocity due to the missing quadratic drag term. I think it is not quadratic drag (exactly), but is instead that atmospheric pressure acting on the leading face of the projectile is not such a good approximation. I think the flow characteristics ahead of the projectile are important. They are what set up the pressure differential across the barrel between the leading face of the projectile and the exit. Solving for that precisely is almost certainly another ball game. I think I have an idea on how to rough it though.

It is undeniable that if drag terms are ignored the simulation will overshoot the exit speed. Especially as the speed of the projectile increases and the mass decreases. At least, for the heavier projectiles they tested within that pressure range, it seems to fit fairly well.

Whether that is a good or bad approximation I consider that to be relative. Now, in relative terms, we can certainly say their model is more accurate than the one I initially proposed because the difference between adiabatic expansion and the expansion due to the choked valve is huge. Its impact is much greater than considering or ignoring friction acting on the projectile (again, for the given pressures, projectile mass, etc.).

It would be interesting to try to fit the data into a new equation that considers those effects. Maybe include something like $-c\dot{x}^n$ and then try a 4-parameter fit. Or add a term in the form of $\rho A( l-x) \ddot x$ as you proposed. Maybe add both and see what fits best. They have plenty of points so I assume the fit must be possible.
Also, the study works with the valve being permanently choked. Maybe it could be done so the valve can change the behavior although I don't know how I would tackle that.

 

[erobz]

It would be interesting to try to fit the data into a new equation that considers those effects. Maybe include something like $-c\dot{x}^n$ and then try a 4-parameter fit. Or add a term in the form of $\rho A( l-x) \ddot x$ as you proposed. Maybe add both and see what fits best. They have plenty of points so I assume the fit must be possible.
Also, the study works with the valve being permanently choked. Maybe it could be done so the valve can change the behavior although I don't know how I would tackle that.

I would like to try to model it as follows (for the resistive force side of the system):

For the projectile:

$$P(x)A - P(z)A - \mu N = m_p \ddot x \tag{1} $$

Now to get the pressure $P(z)$ acting on the leading face, focus on the gas in front of the projectile:

Applying continuity between the inlet and outlet:

$$ \rho(z) \dot z = \rho_{atm} v_o$$

Assuming the air in front of the projectile is undergoing isentropic flow as an ideal gas implies the velocity of the flow at the outlet $v_o$ is given by:

$$ \implies v_o = \left( \frac{P(z)}{P_{atm}}^{\frac{1}{\gamma}} \right) \dot z $$

I would propose a viscous force proportional to some power $n$ of the outlet velocity for a conservative estimate:

$$ F_{\tau} = \beta ~ \dot z^n ~\left( \frac{P(z)}{P_{atm}} \right)^{\frac{n}{\gamma}}$$

For the inertial mass of the flow I'm going to approximate the pressure distribution as linear and the temperature of the gas in the barrel is $T_{atm}$ for the entire body (This is not in line with earlier assumptions about isentropic flow, but trying to account for the variation of density across the barrel would complicate the term significantly). The mass of the flow (treating it as a slug with a single acceleration) being accelerated is given by:

$$ m_{air} \approx \frac{A}{RT_{atm}}\left( \frac{ P(z)+ P_{atm} }{2} \right) ( l-z) $$

Since the coordinates $z$ and $x$ just differ by a constant $a$, $\dot z = \dot x$ and $\ddot z = \ddot x$. Preforming a force balance on the air remaining in the barrel at time $t$:

$$ P(z)A - P_{atm}A - \beta \dot z^n ~ \left( \frac{P(z)}{P_{atm}} \right)^{\frac{n}{\gamma}} = \frac{A}{RT_{atm}}\left( \frac{ P(z)+ P_{atm} }{2} \right) ( l-z) \ddot z \tag{2} $$

Just to check some basic principles assume an isothermal process ($\gamma = 1$) , and a viscous exponent $n = 1$, you can solve this algebraically for $P(z)$:

$$ P(z) = \frac{ P_{atm} A \left( 1 + \frac{1}{2RT_{atm}}(l-z)\ddot z \right) }{ A - \frac{ \beta }{ P_{atm}} \dot z - \frac{A}{RT_{atm}} (l-z) \ddot z } \tag{3} $$

If we assume that $\dot z$ is a constant, the higher order terms drop out ($\ddot z = 0$) and we are left with what seems reasonable to me:

$$ P(z) = \frac{P_{atm}A}{ A - \text{const.}} = \text{constant} > P_{atm} $$

At this point I would substitute (3) into (1) for $P(z)$ with $z = x + a$, and attempt to isolate $\ddot x$ to numerically solve the resulting ODE for the specific case $\gamma = 1, n = 1$.

The more general case of (2) is going to pose some algebraic barriers to that as far as I can tell, but surely there is a path forward.

EDIT: Another possible special case to consider adiabatic process ( which seems realistic ) with $n = \gamma \approx 1.4$. $P(z)$ can be isolated in the same way as (3) under that condition.

I mean this to be combined with whatever is considered to be "the best model" for $P(x)$ on the back end (including the effects of the valve geometry).

 

[Juanda]

I had to read it a few times but I think I got most of it. There is just one thing I can't figure out.

Assuming ideal gas undergoing a polytropic process implies the velocity of the flaw at the outlet $v_o$ is given by:

$$ \implies v_o = \left( \frac{P(z)}{P_{atm}}^{\frac{1}{\gamma}} \right) \dot z $$

Where does that come from? Is it from the previous equation?

Applying continuity between the inlet and outlet:

$$ \rho(z) \dot z = \rho_{atm} v_o$$

Because with $$ \rho(z) \dot z = \rho_{atm} v_o$$ you're saying that the density changes inside the barrel. At $z$ it has a value and at the end of the barrel, it will be $\rho_{atm}$. However, then with $$ \implies v_o = \left( \frac{P(z)}{P_{atm}}^{\frac{1}{\gamma}} \right) \dot z $$ you're saying the density is constant.
Also, if we assume pressure, density, temperature, etc are not constant inside the barrel, then I believe it is not OK to use equations from polytropic processes since they assume quasi-equilibrium at all times. Either we consider we're working with quasi-equilibrium or we don't but using it just sometimes feels strange don't you think?

 

[erobz]

Where does that come from? Is it from the previous equation?

That in concert with Ideal Gas law and Polytropic Process:

Conservation of Mass

$$ \rho(z) \dot z = \rho_{atm} v_o $$

Ideal Gas Law:

$$\rho(z) = \frac{P(z)}{RT(z)} $$

Likewise (assuming outside conditions remain constant):

$$\rho_{atm} = \frac{P_{atm}}{RT_{atm}} $$Polytropic Process:

$$ \frac{T(z)}{T_{atm}} = \left( \frac{P(z)}{P_{atm}} \right)^{\frac{\gamma - 1}{\gamma}} $$

With constant $R$

$$ v_o = \frac{P(z)}{P_{atm}} \left( \frac{T(z)}{T_{atm}} \right)^{-1}$$

Subbing in polytropic process:
$$ v_o = \frac{P(z)}{P_{atm}} \left( \frac{T(z)}{T_{atm}} \right)^{-1}$$

$$ v_o = \frac{P(z)}{P_{atm}} \left( \left( \frac{P(z)}{P_{atm}} \right)^{ \frac{ \gamma - 1}{ \gamma} } \right)^{-1} = \left( \frac{P(z)}{P_{atm}} \right)^{ \frac{1}{ \gamma} }$$

Because with $$ \rho(z) \dot z = \rho_{atm} v_o$$ you're saying that the density changes inside the barrel. At $z$ it has a value and at the end of the barrel, it will be $\rho_{atm}$. However, then with $$ \implies v_o = \left( \frac{P(z)}{P_{atm}}^{\frac{1}{\gamma}} \right) \dot z $$ you're saying the density is constant.

I'm not looking along the length of the barrel with $z$. I'm looking at the state of the gas always at the coordinate $z$, the face of the projectile as it advances. I thought I was saying here is the state of the gas at coordinate $z$ and comparing it with the state it will inevitably end at leaving the barrel at some later time. I'm thinking that the energy of the gas along the barrel per unit volume is constant w.r.t. $z$ at all times $t$. I'm doing this to characterize the outlet velocity as a function of $\dot z$.

Maybe that's not good?

Also, if we assume pressure, density, temperature, etc are not constant inside the barrel, then I believe it is not OK to use equations from polytropic processes since they assume quasi-equilibrium at all times. Either we consider we're working with quasi-equilibrium or we don't but using it just sometimes feels strange don't you think?

If you don't like it, I'm open to suggestions. At that very least, the final reulat seems to be behaving like I'd expect it to.

 

[Juanda]

That in concert with Ideal Gas law and Polytropic Process:

Conservation of Mass

$$ \rho(z) \dot z = \rho_{atm} v_o $$

Ideal Gas Law:

$$\rho(z) = \frac{P(z)}{RT(z)} $$

Likewise (assuming outside conditions remain constant):

$$\rho_{atm} = \frac{P_{atm}}{RT_{atm}} $$

Oh, all right I understand this $$ \rho(z) \dot z = \rho_{atm} v_o $$
I guess we can consider each of the slices of the barrel to be in quasi-equilibrium. I'm not sure if that's valid or not but at least I can track that part of your math now.
I can't keep going today but I'll read your answer again as soon as I get the chance to try to understand all the details.

 

[Juanda]

View attachment 328355

Applying continuity between the inlet and outlet:

$$ \rho(z) \dot z = \rho_{atm} v_o$$

I am still trying to digest all this.
It seems conservation of mass is a pivotal point behind the model you propose. While looking at the equation I started to suspect if it can be applied here the way you did.
I believe you are saying that all the mass pushed from the left by the projectile will immediately exit the barrel.
$$ \rho(z) \dot z = \rho_{atm} v_o$$
That would be true if the gas is incompressible but I don't think we should work with that.
Is that a simplification you consciously took?

Also, I think you assume the gas reaches atmospheric conditions at the end of the barrel. However, that's only true if the barrel is long enough to allow it to expand to that point. To me, it feels more realistic to think that the gas will leave the barrel still being pressurized so it will expand rapidly once it reaches the exit. Forcing the equation so that the exit point has known conditions feels wrong.

I gave the problem another go to try to find what's the pressure in front of the projectile due to the compression of that gas in front of it instead of assuming atmospheric pressure but I couldn't come up with anything meaningful. I still believe the paper in post #3 is a pretty good and scientific approach to the problem. Some of its formulas could be tweaked to try to find a better fit and I miss the optimization part of the design but the overall concept feels convincing.

 

[erobz]

I am still trying to digest all this.
It seems conservation of mass is a pivotal point behind the model you propose. While looking at the equation I started to suspect if it can be applied here the way you did.
I believe you are saying that all the mass pushed from the left by the projectile will immediately exit the barrel.
$$ \rho(z) \dot z = \rho_{atm} v_o$$
That would be true if the gas is incompressible but I don't think we should work with that.
Is that a simplification you consciously took?

I was basing that simplification off of standard analysis for steady-compressible flow. Also the following bit with the adiabatic expansion ( isentropic flow ). I know its not strictly correct. We have friction, unsteady flow, etc....

Also, I think you assume the gas reaches atmospheric conditions at the end of the barrel. However, that's only true if the barrel is long enough to allow it to expand to that point. To me, it feels more realistic to think that the gas will leave the barrel still being pressurized so it will expand rapidly once it reaches the exit. Forcing the equation so that the exit point has known conditions feels wrong.

Then you have to try and model the rapid expansion of the flow at the exit.

I gave the problem another go to try to find what's the pressure in front of the projectile due to the compression of that gas in front of it instead of assuming atmospheric pressure but I couldn't come up with anything meaningful. I still believe the paper in post #3 is a pretty good and scientific approach to the problem. Some of its formulas could be tweaked to try to find a better fit and I miss the optimization part of the design but the overall concept feels convincing.

I'm not saying it's wrong, but paraphrasing the authors of that paper, they feel the discrepancy between the data ( black lines ) and their models lies in failing to model the quadratic drag...i.e. the all the things happening ahead of the projectile. I was just trying to expand... perhaps fool heartedly.