Undergrad Order of summation in series with multiple indices

[user15197573]

TL;DR

Series property

Can someone help me understand why what I wrote is correct? That is: If I have a sequence with double indices and if the summation of the elements modules of this sequence converges (less than infinite) than it does not matter how I make this sum (second line) they are going to be always the same. Thank you.

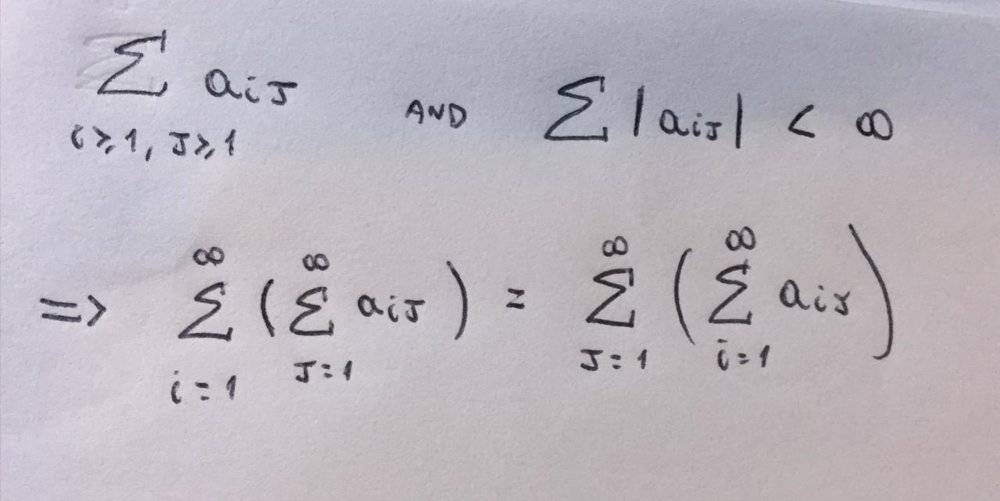edit: Guys, I've just found the answer to this question in another post but I don't know how to delete this.

 

[jedishrfu]

Why not post the answer you found for the benefit of others who may find your post and who may have the same question. This would also allow us to comment on how good an answer it was and perhaps give you some deeper insight to your question.

 

[Svein]

Sounds like a special case of Fubini's theorem to me.

 

[fresh_42]

It is not directly Fubini. We call it "Re-ordering Theorem". Wikipedia lists it as Mertens's theorem (with proof):
https://en.wikipedia.org/wiki/Cauchy_product#Convergence_and_Mertens' theorem
An example why absolute convergence of at least one of the two series is necessary is $\sum_{k=0}^\infty \frac{(-1)^k}{\sqrt{1+k}}\,.$

 

[user15197573]

Why not post the answer you found for the benefit of others who may find your post and who may have the same question. This would also allow us to comment on how good an answer it was and perhaps give you some deeper insight to your question.

I'll take that into consideration in my next post since some people already answered here. Thank you.