Oriented Surfaces & Surface Area: Investigating the Impact

[Trysse]

TL;DR

I have the following question: Does it make a difference for the surface area of a sphere if the sphere is inward- and outward-oriented?

I usually think of a sphere as the set of all points $P_x$, that have the identical distance r to some point $C$ which is the center of the sphere. I calculate the surface area $A$ of the sphere as
$$A=4 \pi (C P_x)^2$$
However, what happens if I think of the distance between the points C and Px not just as a distance but as a vector? If I think of the radius of the sphere as a vector, this vector can either point from the surface of the sphere to the center or from the center to the surface
$$ \vec {CP_x} = \vec{r} = \vec{-r} = \vec{P_x C} $$

Does the direction of the radius (i.e. the orientation of the surface) have an influence on the concept of surface area? I was wondering if it makes sense to say:
$$ A=4π \vec{CP_x}^2=−4π \vec{P_xC}^2 $$

I have done a quick search on Google. However, from what I have found, I got the impression, that the surface area is not really an issue that is considered in the context of oriented surfaces. Or did I just search for the wrong keywords?

https://www.google.com/search?q=ori...rome..69i57.6231j0j4&sourceid=chrome&ie=UTF-8

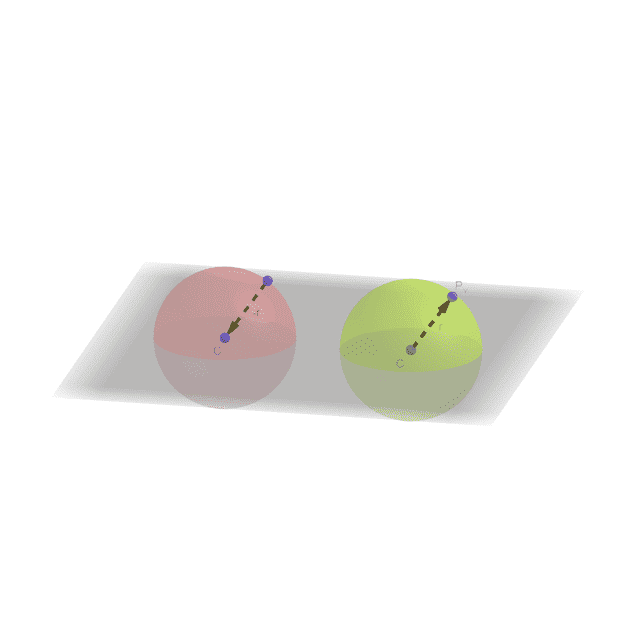
Could I say that the red sphere has a negative surface area while the green sphere has a positive surface area?

 

[hutchphd]

Not to me.
In my world, for any closed surface, the outward normal vector is positive.
This is of course an arbitrary, but adherent, convention.

 

[PeroK]

Could I say that the red sphere has a negative surface area while the green sphere has a positive surface area?

Area is, by definition, positive. That said, you can talked about a signed area:

https://amsi.org.au/ESA_Senior_Years/SeniorTopic3/3f/3f_2content_8.html

 

[Mark44]

P.S: I am unable to make the formula display properly. Can someone help?

Now fixed. There were a couple inconsistencies with left braces not having a matching right brace; i.e., { with ) and { with ].

 

[DaveE]

Area is a scalar value. When you calculate it starting with a vector, you will have to take the magnitude of the vector to create a scalar result. The magnitude of the radius vector doesn't depend on it's direction.

Note that sometimes vectors are used to describe an "area" with the magnitude describing the area and the direction normal to the surface. Like the cross product of vectors, for example. It still doesn't have negative area, but in vector math you might describe the direction as negative, I guess.

 

[hutchphd]

Also in optics the radius of curvature is often given a signed value depending upon the focal point.
And the "vector Area" is useful when talking about flow ("flux") through a surface unambiguously.