Origin of Probabilities in Quantum Mechanics?

[jcap]

The non-normalized wavefunction of a general qubit is given by:
$$|\psi\rangle=A|0\rangle+B|1\rangle.$$
The complex amplitudes $A$ and $B$ can be represented by two arrows in the complex plane:

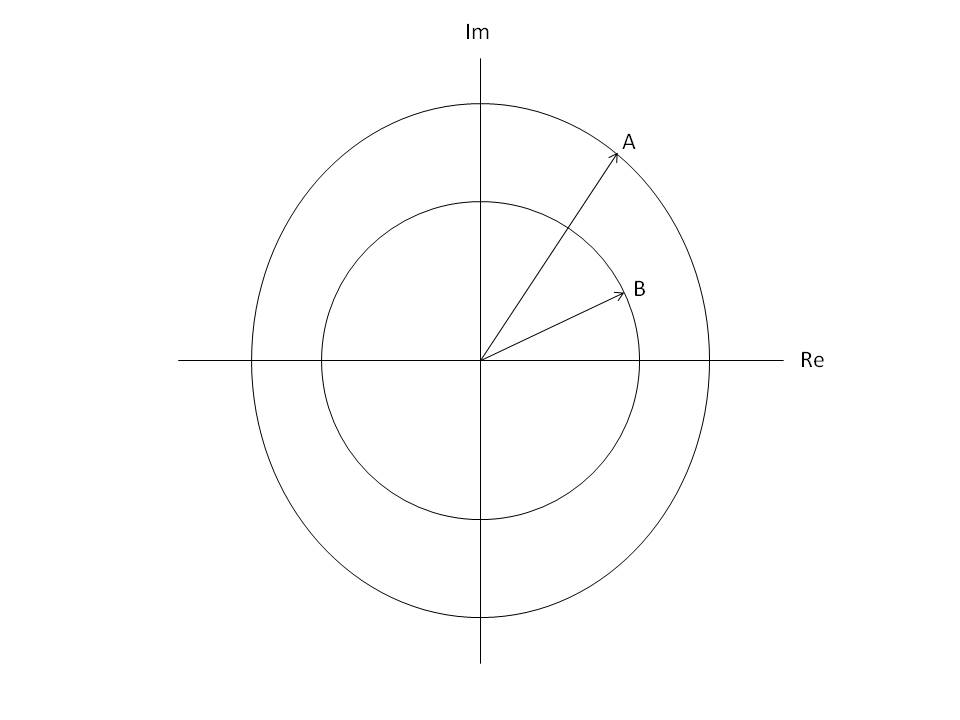
Now the wavefunction can be multiplied by any complex number $R$ without changing the physics. This will cause the arrows $A$ and $B$ to rotate and shrink/expand together with a fixed angle between them.

Therefore two sets of points will be traced out represented by a circle with area $|A|^2$ and a circle with area $|B|^2$. These represent the sets of possible values for the amplitudes $A$ and $B$.

Thus if we become entangled with the qubit then the probabilities of finding ourselves in set $A$ (measuring $0$) or set $B$ (measuring $1$) are given by:
$$P(0)=\frac{|A|^2}{|A|^2+|B|^2}$$
$$P(1)=\frac{|B|^2}{|A|^2+|B|^2}.$$
Does this picture help to understand the origin of probabilities in quantum mechanics?

 

[anuttarasammyak]

Hello. I add that after normalization circle A and circle B are transformed within unit circle. Relative angle between A and B matters not their absolute angle to axis because wavefunctions $\psi$ and $e^{i\alpha}\psi$ express the same state.

So we may improve by making :
$$A=\cos (\theta/2), B=\sin(\theta/2)$$
where $0 \leq \theta \leq \pi$. You see positivity and normalization
$$0 \leq A,B \leq 1,\ \ A^2+B^2=1$$
is satisfied in that form. Also take angle of A is zero and angle of B to A is $\phi$.
$$P(0)=\cos^2 (\theta/2),\ \ P(1)=\sin^2 (\theta/2)$$Four parameters A, angle of A, B and angle of B will be reduced to two, $\theta$ and $\phi$. These two angles $\theta$ and $\phi$ which are interpreted as polar coordinates for unit sphere $r=1$ called Bloch sphere in this context express qubit state.

As for projection of state vector to z axis
Length from |1> pole to the projection
$$cos\theta -(-1)= 2P(0)$$
is |0> probability multiplied by 2.
Length from |0> pole to the projection
$$1-cos\theta = 2P(1)$$
is |1> probability multiplied by 2.

 

[andresB]

Does this picture help to understand the origin of probabilities in quantum mechanics?

I don't think so. You are describing a quantum system, but that do not explain why it has to be that way. I may be misunderstanding your question, though.

 

[jcap]

I don't think so. You are describing a quantum system, but that do not explain why it has to be that way. I may be misunderstanding your question, though.

I was wondering if the redundancy in the magnitude and angle of the overall phase factor implies circular areas of amplitudes associated with the vectors $|0\rangle$ and $|1\rangle$. These areas could provide the "weights" for obtaining the eigenvalues $0$ and $1$.

As I understand it I can normalize $|\psi\rangle$ by either first choosing an $A$ or first choosing a $B$. There are a circular area's worth of $A$s that I can pick or a circular area's worth of $B$s. These areas give the weights for obtaining eigenvalues $0$ or $1$ respectively. Maybe this argument only works with a discrete grid of amplitude values.

 

[PeterDonis]

Does this picture help to understand the origin of probabilities in quantum mechanics?

I don't see how since your picture only gives a way to visualize the numerical values of the probabilities, not why there are probabilities at all in the first place.

 

[jcap]

Correction

Let
$$A=R_Ae^{i\theta_A}$$
$$B=R_Be^{i\theta_B}$$
A general normalized wavefunction is given by:
$$|\psi\rangle=\frac{1}{(R_A^2+R_B^2)^{1/2}}\large[R_Ae^{i\theta_A}+R_Be^{i\theta_B}\large]$$
Assume that I multiply the amplitudes $A$ and $B$ by
$$C=Re^{i\theta}$$
Then the normalized wavefunction becomes
$$|\psi\rangle=\frac{1}{R(R_A^2+R_B^2)^{1/2}}\large[RR_Ae^{i(\theta_A+\theta)}+RR_Be^{i(\theta_B+\theta)}\large]$$
$$|\psi\rangle=\frac{e^{i\theta}}{(R_A^2+R_B^2)^{1/2}}\large[R_Ae^{i\theta_A}+R_Be^{i\theta_B}\large]$$
It seems that the only degree of freedom is a phase angle $\theta$ rather than an area as I asserted above.

 

[anuttarasammyak]

It seems that the only degree of freedom is a phase angle θ rather than an area as I asserted above.

@jcap this $\theta$ has no physical meaning as I said in post #2 so it is convenient to take it as $-\theta_A$ so that phase factor appears only on B.

My post #2 does so, i.e.
$$\cos\frac{\theta}{2}|0>+e^{i\phi}sin\frac{\theta}{2}|1>$$

 

[RUTA]

This is how we explained the origin of probability for the qubit: https://www.mdpi.com/1099-4300/23/1/114 (see Section 3).